선택(Selection) 정렬
선택 정렬은 말 그대로 현재 위치에 들어갈 데이터를 찾아 선택하는 알고리즘이다.
좀더 정확하게 말하자면 무작위 데이터 중 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복하는 것이다.
데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다. 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 보는 것이다.
그리고 '불안정 정렬'이다.
| 특성 | 설명 |
| In-place 알고리즘 | Memory 상에서 필요 시 상호 위치만 변경될 뿐 추가적인 배열 생성이 불 필요함 |
| Unstable 알고리즘 | Stable을 보장할 수 없다. 그 이유는 아래에 설명 |
정렬 방법
선택 정렬의 과정은 다음과 같다.
- 주어진 리스트에서 최솟값을 찾는다.
- 최솟값을 맨 앞 자리의 값과 교환한다.
- 맨 앞 자리를 제외한 나머지 값들 중 최솟값을 찾아 위와 같은 방법으로 반복한다.
즉, 그림으로 보면 다음과 같은 과정을 거친다.

마지막 round 9 를 안하는 이유는 앞 인덱스부터 순차적으로 정렬해나가기 때문에 "N개의 데이터 중 N-1개가 정렬 되어있다"는 것은 결국 마지막 원소가 최댓값이라는 말이다. 이는 정렬이 되어있다는 상태이므로 굳이 정렬해줄 필요 없다.
전체적인 흐름을 보면 다음과 같다.
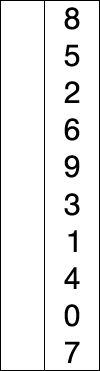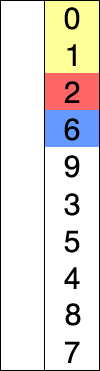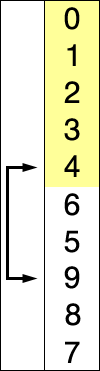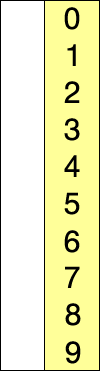

그 외에도 많은 참고 영상들이 있는데, 영상으로 보는 것이 더 쉬울 것 같아 같이 첨부하도록 하겠다.

Selection Sort 구현하기
public class SelectionSort {
public static void sort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min_indx = i;
// 최솟값을 갖고있는 인덱스 찾기
for (int j = i + 1; j < arr.length; j++) {
if (arr[min_indx] > arr[j]) {
min_indx = j;
}
}
// i번째 값과 찾은 최솟값을 서로 교환
swap(arr, min_indx, i);
}
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr, int a, int b) {
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
public static void main(String[] args) {
int[] arr = {5, 3, 7, 1, 6};
sort(arr);
}
}
선택 정렬 장단점
[장점]
1. 추가적인 메모리 소비가 작다.
[단점]
1. 시간복잡도가 O(N^2) 이다.
2. 안정 정렬이 아니다.
단점에 대해 짚고 넘어가보자.
먼저 첫 번째 단점이다. 기본적으로 선택정렬은 O(N^2)의 시간복잡도(time complexity)를 보인다.
공식을 유도해보자면 이렇다.
N이 정렬해야하는 리스트의 자료 수, i가 교환되는 인덱스라고 할 때 loop(반복문)을 생각해보자.
i=1 일 때, 데이터 비교 횟수는 N-1 번
i=2 일 때, 데이터 비교 횟수는 N-2 번
i=3 일 때, 데이터 비교 횟수는 N-3 번
⋮
i=N-1 일 때, 데이터 비교 횟수는 1 번
즉, 다음과 같이 공식화 할 수 있다.

그리고 모든 N에 대하여 다음을 만족하기 때문에 시간복잡도 또한 도출 할 수 있다.

물론 Bubble Sort 와 이론상 같은 시간복잡도를 갖음에도 비교 수행이 상대적으로 적기 때문에 조금 더 빠르긴 하나 그럼에도 좋은 알고리즘은 아니다.
| 알고리즘 | 시간복잡도(최상) | 시간복잡도(평균) | 시간복잡도(최악) | 공간복잡도 |
| 선택 정렬 | O(n^2) | O(n^2) | O(n^2) | O(1) |
두 번째 단점은 안정 정렬이 아니라는 것이다. 즉, Stable 하지 않다는 것. 간단한 예를 들어보겠다.
우리는 다음과 같은 배열을 정렬하고자 한다.
[B1, B2, C, A] (A < B < C)
주의해서 볼 점은 B에 붙어있는 숫자는 임의로 붙인 숫자다. 즉, B1 과 B2는 같은 숫자다.
그럼 순서대로 순회하면서 교환한다면 이렇다.
round 1 : [A, B2, C, B1]
round 2 : [A, B2, C, B1]
round 3 : [A, B2, B1, C]
이렇게 초기의 B1 B2의 순서가 뒤 바뀐 것을 볼 수 있다.
이러한 상태를 불안정 정렬이라고 하는데 문제가 되는 이유는 예로들어 학생을 관리하고자 할 때, 성적순으로 나열하되, 성적이 같으면 이름을 기준으로 정렬하고 싶다고 할 때. 즉, 정렬 규칙이 다수이거나 특정 순서를 유지해야 할 때 문제가 될 수 있다.
[(가영, 60), (가희, 60), (찬호, 70), (동우, 45)] 이렇게 리스트가 존재한다고 생각해보자. 성적순이되, 성적이 같다면 이름순으로 정렬해야 한다고 했다.
그러면 보통 이름을 일단 정렬을 해놓을 것이다.
<이름 정렬 순>
[(가영, 60), (가희, 60), (동우, 45), (찬호, 70)]
그 다음에 '성적 순'으로 정렬 할 것이다. 만약 선택 정렬을 하면 어떻게 되는지 보자.
round 1 : [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)]
round 2: [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)]
round 3: [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)]
이렇게 '가희'보다 '가영'이 앞에 있어야 함에도 순서가 바뀌어 버린 것을 볼 수 있다.
정리
선택 정렬의 경우 정렬 알고리즘의 기초다보니 대부분 거품 정렬(Bubble Sort), 삽입 정렬(Insertion Sort) 과 함께 많이 배운다. 물론 성능상 좋지는 못하더라도 이러한 알고리즘들을 확실하게 익혀야 좀 더 고급스러운 정렬들을 이해 할 수 있다.
테스트 한 결과 selection sort는 5초대에 자리하고 있다. (컴퓨터의 환경에 따라 달라질 수 있다) 이후에 아래 알고리즘들을 모두 구현해볼 것이다.
또한 각 정렬 알고리즘 별 시간 복잡도와 평균 정렬 속도는 다음과 같다.

참고