버블(Bubble) 정렬
두 개의 인접한 원소를 비교하여 정렬하는 방식이다.
왜 Bubble 이라는 이름이 붙었는지 찾아보니 정렬 과정에서 원소의 이동이 마치 버블이 수면위로 올라오는 것 같다고 해서 버블(Bubble) 이라는 이름이 붙었다고 한다...
정렬 방식 중 가장 쉬우니 일단 버블 정렬에 대한 특징만 짚고 넘어가보자.
버블 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다. 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 보는 것이다. 이는 선택정렬과도 같은 부분이다.
그리고 이전에 다뤘던 선택 정렬과는 달리 버블 정렬은 앞에서부터 차례대로 비교하기 때문에 '안정 정렬'이기도 하다.
| 특성 | 설명 |
| In-place 알고리즘 | Memory 상에서 필요 시 상호 위치만 변경될 뿐 추가적인 배열 생성이 불필요 |
| Stable 알고리즘 | 구현하기 나름이나, 기본적으로 값이 같으면 정렬 순서를 바꾸지 않는다. |
정렬 방법
버블 정렬의 전체적인 과정은 이렇다. (오름차순을 기준으로 설명)
- 앞에서부터 현재 원소와 바로 다음의 원소를 비교한다.
- 현재 원소가 다음 원소보다 크면 원소를 교환한다.
- 다음 원소로 이동하여 해당 원소와 그 다음원소를 비교한다.
즉, 그림으로 보면 다음과 같은 과정을 거친다.

이 때, 각 단계를 진행 할 때마다 뒤에서부터 한 개씩 정렬되기 때문에, 단계가 진행 될 때마다 한 번씩 줄면서 비교하게 된다.
한마디로 정리하자면 이렇다.
- 총 단계는 배열 크기 - 1 번 진행되고,
- 각 라운드별 비교 횟수는 배열 크기 - 라운드 횟수 만큼 비교한다.
전체적인 흐름을 보자면 다음과 같은 형태로 정렬 한다.
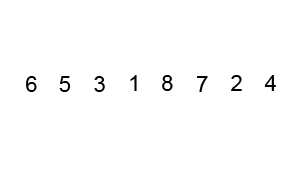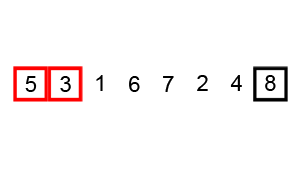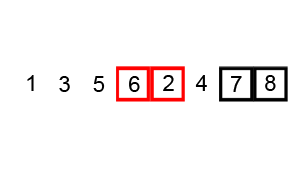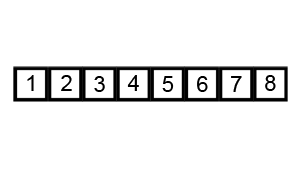

그 외에도 많은 참고 영상들이 있는데, 영상으로 보는 것이 더 쉬울 것 같아 같이 첨부하도록 하겠다.

Bubble Sort 구현하기
public class BubbleSort {
public static void sort(int[] arr) {
// round는 배열 크기 - 1 만큼 진행됨
for (int i = 1; i < arr.length; i++) {
// 각 라운드별 비교횟수는 배열 크기의 현재 라운드를 뺀 만큼 비교함
for (int j = 0; j < arr.length - i; j++) {
// 현재 원소가 다음 원소보다 클 경우 서로 원소의 위치를 교환한다.
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] arr = {3, 1, 4, 6, 8, 2};
sort(arr);
}
}장점 및 단점
[장점]
1. 추가적인 메모리 소비가 작다.
2. 구현이 매우 쉽다.
3. 안정정렬이 가능하다.
[단점]
1. 다른 정렬 알고리즘에 비해 교환 과정이 많아 많은 시간을 소비한다.
시간복잡도
위 그림에서 볼 수 있듯, 초기 배열에서 3과 5의 경우 원래 해당 자리에 맞는 위치지만, 교환과정에서 중간에 한 번씩 맞지 않은 자리임에도 이동하게 된다.
또한 다른 정렬 알고리즘보다 값 교환 과정이 많기 때문에 그만큼 효율성도 떨어진다. 구현하기 쉬움에도 사실상 쓰이지 않는 정렬 방법이기도 하다.
버블 정렬의 평균 시간 복잡도 또한 O(N^2)의 시간 복잡도를 갖는다.
공식을 유도해보자면 이렇다.
N이 정렬해야하는 리스트의 자료 수, i가 라운드라고 할 때 loop(반복문)을 생각해보자.
i=1 일 때, 데이터 비교 횟수는 N-1 번
i=2 일 때, 데이터 비교 횟수는 N-2 번
i=3 일 때, 데이터 비교 횟수는 N-3 번
⋮
i = N-1 일 때, 데이터 비교 횟수는 1 번
즉, 다음과 같이 일반화하여 공식으로 만들 수 있다.


즉, 시간복잡도는 O(N^2)이다.
| 알고리즘 | 시간복잡도(최상) | 시간복잡도(평균) | 시간복잡도(최악) | 공간복잡도 |
| 버블 정렬 | O(n) | O(n^2) | O(n^2) | O(1) |
버블 정렬 최적화
다만, 하나 포인트를 짚고 가자면 최선의 경우(Best Case)일 경우다. 버블 정렬의 경우 크게 두 가지로 나뉘는데, 위 처럼 일반적인 구현의 경우에는 최선의 경우에도 O(N^2) 이다. 비교수행에 있어 이미 정렬되었더라도 각 라운드별로 반복 비교를 하기 때문이다.
하지만, 여기서 최선의 경우 O(N) 으로 만들 수 있는 방법이 있다.
바로, 각 라운드에서 비교수행을 할 때 원소가 교환되지 않는다면, 즉 swap이 발생하지 않는다면 이는 이미 정렬된 데이터라는 의미이기 때문에 정렬을 종료하면 되는 것이다. 즉, 각 라운드에서 비교수행을 했는지를 판단할 수 있는 변수를 하나 두면 되는 것이다.
수정한 코드는 다음과 같다.
public class BubbleSort {
public static void sort(int[] arr) {
// round는 배열 크기 - 1 만큼 진행됨
for (int i = 1; i < arr.length; i++) {
boolean swapped = false;
// 각 라운드별 비교횟수는 배열 크기의 현재 라운드를 뺀 만큼 비교함
for (int j = 0; j < arr.length - i; j++) {
/*
* 현재 원소가 다음 원소보다 클 경우
* 서로 원소의 위치를 교환하고
* 비교수행을 했다는 표시로 swapped 변수를 true로 변경한다.
*/
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
swapped = true;
}
}
/*
* 만약 swap된적이 없다면 이미 정렬되었다는 의미이므로
* 반복문을 종료한다.
*/
if(swapped == false) {
break;
}
}
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] arr = {3, 1, 4, 6, 8, 2};
sort(arr);
}
}이렇게 하면, 성능을 조금 개선시켜 이미 정렬된 경우 첫 라운드에서 탐색을 하고 바로 종료가 된다.
때문에 가끔 검색해보면 Bubble Sort 의 최선의 경우가 O(N)으로 표기하기도 하고, O(N^2) 으로 표기하기도 하는데, 일반적으로 swap 여부를 판단 할 수 있는 변수를 두지 않고 하는 구현의 경우는 O(N^2), swap여부를 판단할 수 있는 변수를 둔 경우 O(N)이라고 보면 된다.
정리
버블정렬의 경우 사실상 거의 쓰이지는 않는 정렬 알고리즘이지만, 반대로 가장 기초적인 정렬 알고리즘이기도 하다. 보통 정렬 알고리즘에 대해 배우면 버블정렬부터 배울 것이다.
하지만 삽입정렬이나 선택정렬과 같은 O(N^2) 의 시간복잡도를 갖는다 하더라도 버블정렬의 교환횟수가 평균적으로 더 많기 때문에 실질적으로는 삽입, 선택 정렬보다 더 많은 시간이 걸린다.
정렬 알고리즘들의 정렬 별 성능표는 아래와 같다..
테스트 한 결과로 Bubble sort는 29초대에 자리하고 있다. (컴퓨터의 환경에 따라 달라질 수 있다) 테스트한 정렬 알고리즘 중 가장 좋지 않은 성능을 보이고 있다.
또한 각 정렬 알고리즘 별 시간 복잡도와 평균 정렬 속도는 다음과 같다.

이후에 차근차근 구현해보겠지만, 각 알고리즘마다 최상과 평균 시간복잡도와 안정성은 어느정도 알고있는 것이 좋다.
만약 정렬 알고리즘에서 버블정렬을 배울 때 이렇게 swap에 대한 flag변수를 두지 않는다면, 최선의 경우에도 O(N^2)의 시간 복잡도를 갖기 때문에 반드시 확인해보는 것이 좋다.
참고
- https://evan-moon.github.io/2018/10/13/sort-algorithm/
- https://velog.io/@mng051/%EB%8C%80%ED%91%9C%EC%A0%81%EC%9D%B8-%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98#%EC%82%BD%EC%9E%85-%EC%A0%95%EB%A0%AChttps://hongjw1938.tistory.com/28
- https://st-lab.tistory.com/195