Shell Sort(셸 정렬)
셸 정렬은 'Donald L. Shell' 이 제안한 방법으로, 삽입 정렬(Insertion Sort)를 보완한 방식이다.
삽입 정렬의 문제점은 무엇이 있을까?
삽입 정렬은 각 데이터가 삽입될 적절한 위치를 찾기 위해서 인접한 데이터와의 여러 번의 비교 과정을 거쳐야만 한다.
즉, 만약 삽입되어야 할 위치가 현재 위치에서 상당히 멀리 떨어진 곳이라면 많은 이동을 해야만 제자리로 갈 수 있다.
그런데, 이 삽입 정렬은 Nearly Sorted 상태의 데이터라면 O(n)에 가까운 매우 빠른 성능을 보여준다는 장점이 있다.
그래서 셸 정렬은 기존의 삽입 정렬을 수행하기 전에 전체 데이터를 Nearly Sorted 형태로 만들면 기존의 삽입 정렬을 그대로 처음부터 적용하는 것보다 더 좋은 성능을 발휘할 수 있다는 점에 착안한 것이다.
셸 정렬의 특징은 다음과 같다.
| 특성 | 설명 |
| In-place 알고리즘 | Memory 상에서 필요 시 상호 위치만 변경될 뿐 추가적인 배열 생성이 불 필요함 |
| Unstable 알고리즘 | 같은 값의 데이터의 기존 순서 유지를 보장할 수 없다. |
삽입 정렬의 시간 / 공간 복잡도는 아래와 같다.
| 알고리즘 | 시간복잡도(최상) | 시간복잡도(평균) | 시간복잡도(최악) | 공간복잡도 |
| 셸 정렬 | O(n) | O(nlogn) | O(n^2) | O(1) |
대략적인 과정은 다음과 같다.
- 먼저 정렬해야 할 리스트를 일정한 기준에 따라 분류
- 연속적이지 않은 여러 개의 부분 리스트를 생성
- 각 부분 리스트를 삽입 정렬을 이용하여 정렬
- 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든 후에 알고리즘을 반복
- 위의 과정을 부분 리스트의 개수가 1이 될 때까지 반복
셸 정렬의 동작 방식은 삽입 정렬과 동일하다.
그런데, 기존 삽입 정렬은 삽입 위치를 찾기 위해 인접 값들끼리만 비교했다면 셸 정렬은 Gap 을 두어 인접하지 않은 값들 끼리 비교한다.
그리고 그 Gap을 줄여가는데, Gap이 1이 되면 삽입 정렬과 동일한 상태로 동작하게 된다. Gap이 1이 되기 전까지 전체 데이터는 Nearly Sorted 상태가 되는 것이다.
셸 정렬이 Unstable한 이유는 이 Gap을 통해 인접하지 않은 값 끼리의 교환이 일어날 수 있기 때문이다.
이제 셸 정렬의 동작 과정을 살펴보자.
초기 상태의 배열이 아래와 같다.

여기서, 정렬은 0번 부터 시작하지만 0번의 데이터와 비교할 값은 0+k번째 데이터이다. 이때, k를 ‘간격(gap)’ 이라고 한다.
- 간격의 초깃값: (정렬할 값의 수) / 2
- 생성된 부분 리스트의 개수는 gap과 같다.
① k = (10 / 2) = 5 일 때, 비교 및 정렬 후 상태
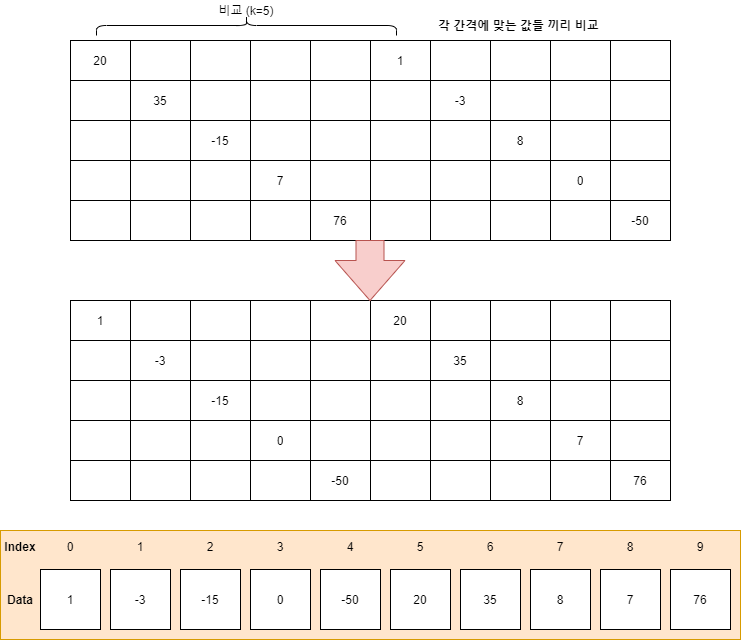
1차적으로 정렬을 완료하였으니 Gap줄여준다. Gap은 여기서 기존의 값에서 절반으로 줄인다. 되도록 홀수가 나오도록 하는 것이 좋다. 그러니 5 / 2 = 2.5 이므로 반올림하여 3으로 만든다.
현재의 Gap = 3 이다.
② k = 3 일 때, 비교 및 정렬 후 상태
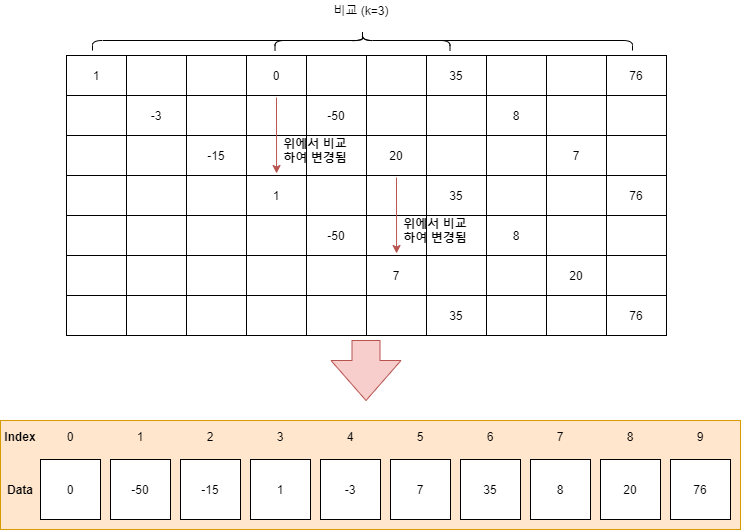
마지막으로 Gap이 1이 되어 삽입 정렬을 시도하면 전체적으로 Nearly Sorted 상태가 되어 매우 빠른 성능으로 전체 데이터 정렬이 완료된다.
③ 마지막 Gap=1일 때, 삽입 정렬을 시도한 결과

여기까지 셸 정렬의 방법을 모두 알아보았다. 이제 코드로 구현하는 방법을 알아보자. 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class ShellSort {
public static void shellSort(int[] arr) {
// Gap에 따라 정렬하기 때문에 Gap을 이용한 반복문 생성
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
// Gap의 크기에 맞게 최초 정렬을 시작할 기준을 지정하여 반복문 형성
for (int i = gap; i < arr.length; i++) {
// i에 지정된 값에 해당하는 값은 정렬을 대비해 미리 지정해 둔다.
int newElement = arr[i];
int j = 0;
for (j = i - gap; j >= 0; j -= gap) {
if (arr[j] < newElement) {
arr[j + gap] = arr[j];
} else {
break;
}
}
// 기존에 저장한 배열 값을 저장
arr[j + gap] = newElement;
}
}
}
public static void main(String[] args) {
// Test code
int[] arr = {20, 35, -15, 7, 76, 1, -3, 8, 0, -50};
shellSort(arr);
System.out.println("셸 정렬: " + Arrays.toString(arr));
}
}
|
cs |
마지막으로, Gap을 어떻게 결정하여 정렬하는 것이 좋은지에 대한 것이다.
위의 예시에서는 Gap Sequence를 단순히 전체 배열의 크기에서 시작해 2로 나누어가며 진행했지만, 실제로는 연구에 의해 또는 실험적으로 Best Gap Sequence 라는 것이 제공되고 있다.
위키피디아를 참고한다면 여러 가지 방법론이 있는 것을 확인할 수 있지만, 대표적으로 Knuth Sequence와 Ciura Sequence에 대해 간단히 언급하면 다음과 같다.
Knuth Sequence는 Gap이 다음과 같은 순서로 결정된다.
1, 4, 13, 40, 121 ...
수식은 어렵지 않다. (3^K - 1 / 2) 로 결정되며 전체 배열의 크기가 N이라면 Gap은 N/3 보다 작은 수 중 가장 큰 값으로 결정 된다.
즉, 만약 배열의 크기가 100이라면, 33.333이므로 Gap은 13부터 시작해 4, 1로 내려가면서 마무리한다.
Ciura Sequence는 Gap이 다음과 같은 순서로 결정된다.
1, 4, 10, 23, 57, 132, 301, 701 ...
별도의 수식이 정해져 있지 않고, 실험적으로 결정된 값이다. 701 이후의 값은 딱히 나와있지 않다. 현재 배열의 크기보다 작은 수 중 가장 큰 값부터 시작하여 1까지 내려가면 된다.