그래프 탐색
그래프는 기본적으로 각 정점들이 어떠한 연관 관계를 갖고 있는지를 나타내는 자료구조 이다. 그래프는 가장 기본적이고 유연한 구조로 관계를 나타낼 수 있다. 많은 문제들 중 그래프로 해결 가능한 문제가 50% 정도 된다고 이야기하는 엔지니어도 있다. (참고)
해결 가능한 문제들의 예시를 알아보자. 어떠한 것들이 특히 해결이 가능할까?
ⓐ 네트워크 : 우리가 사용하는 컴퓨터는 인터넷으로 연결된다. 각 컴퓨터나 네트워크 장비를 정점(vertex , node)로 연결을 간선(edge)로 본다면 그래프로 표현이 가능하다.
ⓑ 경로 찾기 : 특정 위치 간 가장 짧은 경로 / 긴 경로를 그래프를 이용해 찾을 수 있다. 구글 맵 또한 이러한 응용을 한 것이며, 게임 내 NPC 등의 모델도 이를 통해 움직임이 구현된다.(이외 GPS, High Frequency Trading 등에도 활용)
ⓒ 순서 확인 : 특정 정점을 할 일이라고 본다면 그에 대한 연결을 통해 순서를 지정할 수 있다.(위상 정렬 예시)
ⓓ 연결성 확인 : 전자 회로 내 특정 회로가 상호 연결되어 있는지 확인하는 경우 등에 사용
이러한 문제들을 해결하는데 그래프를 어떻게 활용할 것인가? 이번 포스팅에서는 우선 그래프를 탐색하는 방법에 대해서 알아보자.
그래프 탐색에는 대표적으로 너비 우선 탐색(BFS, Breadth First Search), 깊이 우선 탐색(DFS, Depth First Search)가 있다. 여기서는 넓이 우선 탐색(BFS)을 알아보자.
깊이 우선 탐색(DFS, Depth First Search)

깊이 우선 탐색은 가장 쉽게 비교할 수 있는 것은 이전 포스팅의 트리(Tree) 구조의 순회(in/pre/post Order) 이다.
그래프도 비슷한 방식으로 동작한다고 보면 되는데, 최초 시작 정점에서 가장 먼저 이어져 있는(간선으로 연결된) 정점을 하나 찾고 해당 정점에 또 인접한 정점을 찾아 더 이상 깊이 갈 수 없을 때까지 탐색한 뒤 돌아오는 방식이다.
트리와의 큰 차이점은, 그래프는 순환(Cycle)할 수 있다는 것이다. 그래서, 순환 탐지(Cycle Detection)를 할 수 있도록 추가적인 기능을 구현해야 한다는 것이다.
BFS와의 큰 차이점은, DFS는 탐색을 한 뒤 이전의 정점으로 돌아온다는 것이다. 이것을 백트래킹(Backtracking)이라고 한다. 이것을 이용하여 다양한 문제에 활용할 수 있다.(이에 대해서는 추후 포스팅)
그림으로 보기

STEP 1: A를 시작노드로 하곘습니다.
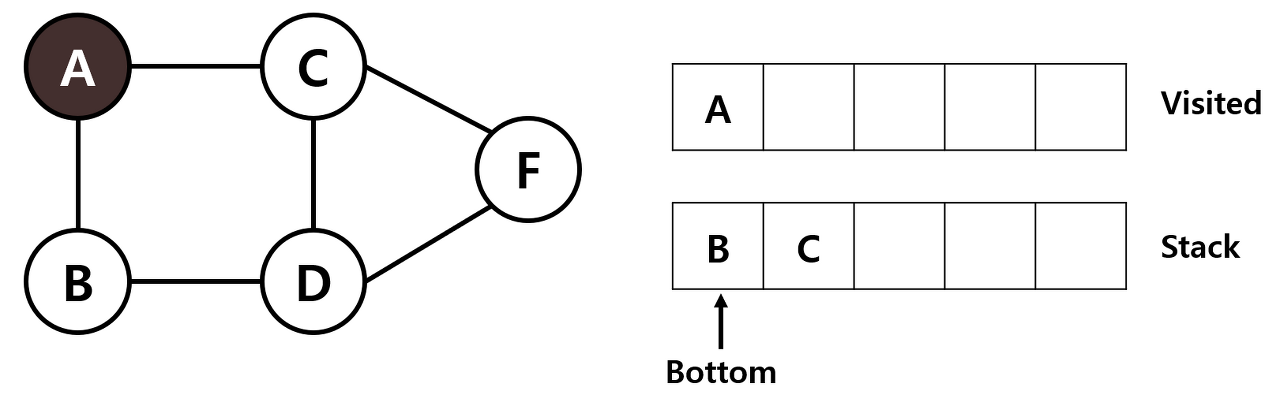
STEP 2: A에 인접한 B, C가 스택에 저장됩니다.

STEP 3: 스택의 맨 위에 있는 C를 꺼내서 Visited 배열에 넣습니다. C의 인접한 노드인 D, F가 스택에 저장됩니다.

STEP 4: 스택의 맨 위에 있는 F를 꺼내서 Visited 배열에 넣습니다. F에 인접한 노드인 D는 이미 Stack에 있으므로 넘어갑니다.

STEP 5: 스택의 맨 위에 있는 D를 꺼내서 Visited 배열에 넣습니다. D에 인접한 C, F는 Visited 배열에 있으며 B는 스택에 있으므로 넘어갑니다.
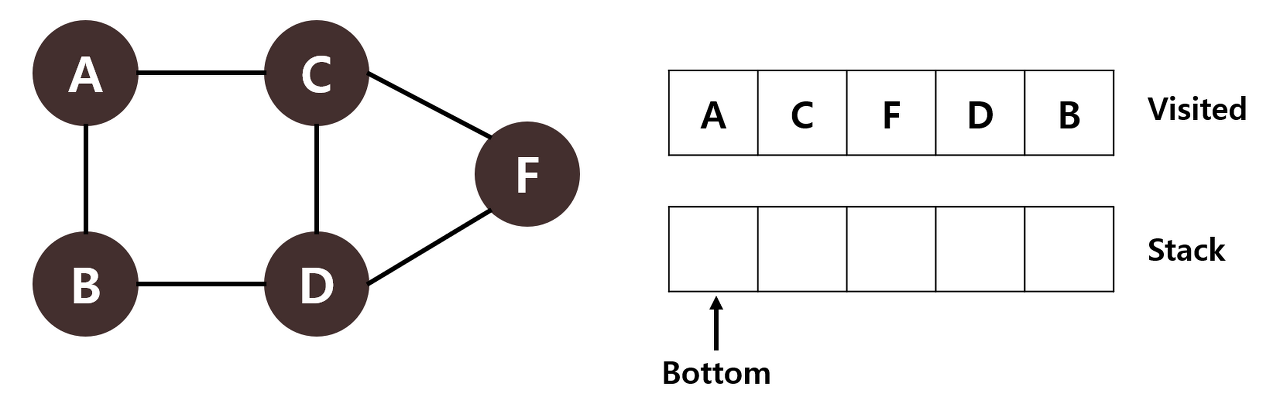
STEP 6: 스택의 맨 위에 있는 B를 꺼내서 Visited 배열에 넣습니다. 스택이 비어있으므로 탐색을 종료합니다.
DFS를 사용하는 예시
그래프의 순환이 있는지 확인하는 경우 많이 쓰인다. BFS로도 가능하지만 DFS가 더 메모리 효율적이다. 기타 경로 찾기, 위상 정렬, 미로 찾기 등등 다양한 예시에 사용될 수 있다.
하지만 최단 경로를 찾을 때는 BFS를 기반으로 탐색해야 한다.. BFS는 최단 경로를 즉각적으로 보장해주면서 탐색을 할 수 있지만 DFS는 그렇지 못한 경우가 있기 때문이다. (BFS 포스팅 참조)
아래 예시를 보자.

만약 우리가 주황색으로 칠해진 곳에서 빨간색으로 칠해진 곳으로 가고자 한다고 할 때, 유일한 경로는 파란 화살표와 빨간 화살표가 있을 수 있다.(다른 것도 가능하지만 대표적으로)
그럼 BFS로 탐색을 하면 빨간 부분, 파란 부분 인접 정점을 동시에 차례 대로 탐색을 하게 되며 시작점이 고정이라서 무조건 모든 인접 정점이 최소의 경우로만 이동하도록 보장이 된다.
그래서 BFS로 탐색 시, 원하는 위치에 도달했다면 추가 탐색을 그만두어 빠르게 문제를 해결할 수 있게 된다.
그런데 DFS로 탐색을 하면, 상단의 빨간색 부분 부터 우선 탐색이 이루어질 수 있다. 하지만 이 경로는 최소 경로라는 보장이 불가능하다! 실제 위의 예시에서는 최소 경로가 아니다.
보장을 하기 위해서는 이미 방문한 경로의 정점을 미 방문 상태로 전환하고 다른 모든 동일 위치에 도달할 수 있는 경우를 체크해야 하는데, 그것은 DFS가 아니라 Brute Force 방법이 된다. 그러면 문제를 푸는데, 시간복잡도가 높아져 문제를 풀 수 없게 된다.
(DFS, BFS는 기본적으로 이미 방문한 정점을 다시 방문하지 않아야 함!)
DFS 장단점
⭕ DFS 장점
- 현 경로상의 노드를 기억하기 때문에 적은 메모리를 사용한다.
- 찾으려는 노드가 깊은 단계에 있는 경우 BFS 보다 빠르게 찾을 수 있다.
❌ DFS 단점
- 해가 없는 경로를 탐색 할 경우 단계가 끝날 때까지 탐색한다. 효율성을 높이기 위해서 미리 지정한 임의 깊이까지만 탐색하고 해를 발견하지 못하면 빠져나와 다른 경로를 탐색하는 방법을 사용한다.
- DFS를 통해서 얻어진 해가 최단 경로라는 보장이 없다. DFS는 해에 도착하면 탐색을 종료하기 때문이다.
구현 방법
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)
init()
For each u ∈ G
u.visited = false
For each u ∈ G
DFS(G, u)스택 또는 재귀 방식을 이용하여 구현할 수 있다. ( 스택 없이 인접 행렬을 통해 구현도 가능 여기 참조)
스택은 FILO(First-In, Last-Out) 방식이기 때문에 인접한 정점이 우선이 아닌 더 멀리 있는(인접 정점의 끝) 정점을 우선 탐색한 뒤 돌아올 수 있다. 큐는 FIFO라서 인접 정점을 우선하여 탐색하므로 쓸 수 없다. 큐는 BFS에 사용
재귀 방식으로 진행하는 것 또한 가능하다. 재귀 자체가 내부적으로 Stack을 사용하는 방식이기 때문이다. 둘 중에선 재귀 방식이 더 많이 쓰인다. 더욱 구현이 간단하기 때문이다.
시간복잡도 : O(V+E), V는 정점 / E는 간선의 개수로 그 개수에 따라 전체 탐색에 시간이 소요된다.(인접 행렬은 O(V^2))
공간복잡도 : O(V), 최악의 경우, 정점이 1열로 이어져 전체 정점의 수 만큼 스택이 쌓일 수 있다.
코드
재귀방식과 스택 사용 방식을 모두 구현하여 살펴보자.
아래와 같이 구현할 수 있다. 주석 내용을 확인하며 코드를 이해하면 쉽게 이해할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
|
public class Graph {
public static void main(String[] args){
Graph g = new Graph(6);
g.addEdge(0, 1); // 0 -> 1 연결
g.addEdge(0, 5); // 0 -> 5 연결
g.addEdge(1, 2); // 1 -> 2 연결
g.addEdge(1, 3); // 1 -> 3 연결
g.addEdge(1, 4); // 1 -> 4 연결
g.addEdge(2, 0); // 2 -> 0 연결
g.addEdge(3, 4); // 3 -> 4 연결
g.addEdge(4, 2); // 4 -> 2 연결
g.dfs();
}
private int v; // 정점의 개수
private LinkedList<Integer> adj[]; // 인접 리스트
public Graph(int v){
this.v = v;
this.adj = new LinkedList[v];
for(int i=0; i < v; i++){
adj[i] = new LinkedList<>();
}
}
// Source 정점에서 Dest 정점을 이어주는 메소드
public void addEdge(int s, int d){
this.adj[s].add(d);
}
// DFS를 수행하는 메소드
public void dfs(){
// 전체 정점이 최초에는 visited를 false 설정
boolean visited[] = new boolean[this.v];
// 반복문 기반으로 Disconnected Graph라도 전체 탐색이 가능
// 재귀 기반 DFS 수행 시작
for(int i=0; i < this.v; i++){
if(!visited[i]){
dfs_recurvise(i, visited);
}
}
System.out.println();
// 스택 기반 수행을 위해 다시 false로 초기화
visited = new boolean[this.v];
// 스택 기반 DFS 수행 시작
for(int i=0; i < this.v; i++){
if(!visited[i]){
dfs_stack(i, visited);
}
}
}
// DFS 재귀 수행 메소드
public void dfs_recurvise(int v, boolean visited[]){
visited[v] = true;
System.out.print(v + " ");
// 방문하지 않은 인접 정점을 모두 찾아 우선 탐색 수행
Iterator<Integer> i = this.adj[v].listIterator();
while(i.hasNext()){
int n = i.next();
if(!visited[n]){
dfs_recurvise(n, visited);
}
}
}
// DFS 스택 수행 메소드
public void dfs_stack(int start, boolean visited[]){
Stack<Integer> stack = new Stack<>();
stack.push(start);
while(!stack.isEmpty()){
int v = stack.pop();
System.out.print(v + " ");
// 방문하지 않은 인접 정점을 모두 찾아 우선 탐색 수행
Iterator<Integer> i = this.adj[v].listIterator();
while(i.hasNext()){
int n = i.next();
if(!visited[n]){
visited[n] = true;
stack.push(n);
}
}
}
}
}
/*결과
0 1 2 3 4 5
0 5 1 4 3 2
Process finished with exit code 0
결과가 아래가 다른 이유는 print 시점 때문
재귀는 탐색 시에 print하고 스택 시에는 stack에서 뺄 때 print함
중요한 것은 모든 것이 탐색 되느냐로 본다.
*/
|
cs |
깊이 우선 탐색의 응용
깊이 우선 탐색을 활용하는 경우는 여러 가지가 있다. 대표적인 예시를 아래와 같이 살펴보자.
① 최단 경로 찾기 및 최소 스패닝 트리
② 순환 탐지
③ 위상 정렬
④ Puzzle 풀이(하나의 solution 찾기)
DFS는 이외에도 굉장히 많이 쓰인다. 익혀두고 익숙해지는 것이 중요하다.
참고) DFS와 백트래킹(Backtracking)의 차이
DFS는 기본적으로 그래프 형태 자료구조에서 모든 정점을 탐색할 수 있는 알고리즘 중 하나이다. 깊이를 우선적으로 탐색하기에 재귀 또는 스택을 이용한다.
재귀를 이용하여 탐색을 수행한다는 부분에서 완전탐색 알고리즘의 재귀 / 백트래킹(Backtracking)과 유사한 측면이 보여 혼란이 올 수 있다.
그런데, 재귀라는 것은 말 그대로 스스로의 함수(또는 메소드)를 호출하는 방식을 의미하는 것이므로 DFS가 재귀라는 방식을 이용해 탐색을 수행하는 것으로 하나의 방식이라고 이해하면 된다.
또한 백트래킹(Backtracking)은 재귀를 통해 알고리즘을 풀어 가는 기법 중 하나로 가지치기(Pruning)을 통해서 탐색을 시도하다가 유망하지 않으면 추가 탐색을 하지 않고 다른 해를 찾는 방법이다.
DFS는 기본적으로 모든 노드를 탐색하는 것이 목적이지만 상황에 따라서 백트래킹 기법을 혼용하여 불 필요한 탐색을 그만두는 것 또한 가능하다.
즉, DFS와 백트래킹은 유사한 부분이 있지만 기본적으로 사용 목적이 다르지만 두 기법을 혼용하여 사용하는 것이 가능하다. 완전히 다른 개념이 아니라 재귀 호출을 통한 기법 중 하나 이기 때문이다.
DFS vs BFS 탐색 차이
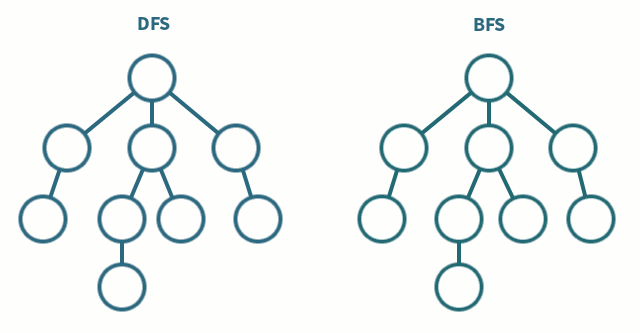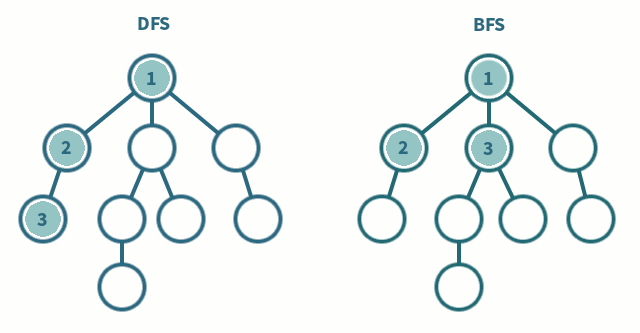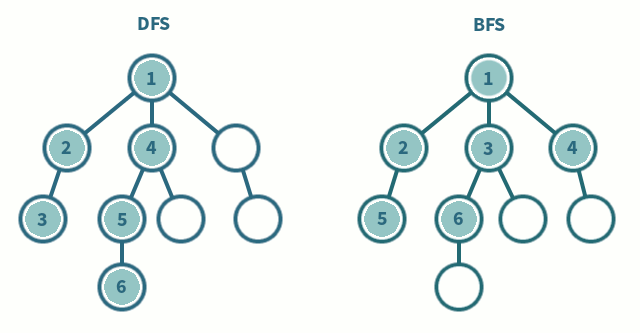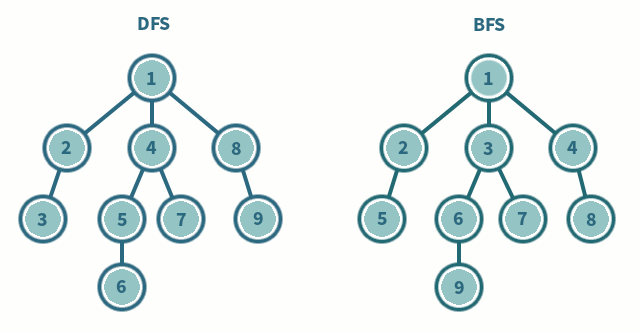
Figure 2. 트리에서 DFS, BFS 탐색 차이
- DFS는 스택(혹은 재귀), BFS 큐를 사용한다.
- BFS는 재귀적으로 동작하지 않는다.
But 문제를 푸는 입장에서는 다음과 같은 구분점이 필요하다.
- 최단 거리 문제를 푼다면 BFS를 사용
- 이동할 때마다 가중치가 붙어서 이동한다거나 이동 과정에서 여러 제약이 있을 경우 DFS로 구현하는 것이 좋다.
참고
https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html
https://heytech.tistory.com/56
https://covenant.tistory.com/132
https://hongjw1938.tistory.com/41#

