[알고리즘-기초] 그래프 탐색(너비 우선 탐색 - BFS)

그래프 탐색

그래프는 기본적으로 각 정점들이 어떠한 연관 관계를 갖고 있는지를 나타내는 자료구조 이다. 그래프는 가장 기본적이고 유연한 구조로 관계를 나타낼 수 있다. 많은 문제들 중 그래프로 해결 가능한 문제가 50% 정도 된다고 이야기하는 엔지니어도 있다. (참고)

해결 가능한 문제들의 예시를 알아보자. 어떠한 것들이 특히 해결이 가능할까?

ⓐ 네트워크 : 우리가 사용하는 컴퓨터는 인터넷으로 연결된다. 각 컴퓨터나 네트워크 장비를 정점(vertex , node)로 연결을 간선(edge)로 본다면 그래프로 표현이 가능하다.
ⓑ 경로 찾기 : 특정 위치 간 가장 짧은 경로 / 긴 경로를 그래프를 이용해 찾을 수 있다. 구글 맵 또한 이러한 응용을 한 것이며, 게임 내 NPC 등의 모델도 이를 통해 움직임이 구현된다.(이외 GPS, High Frequency Trading 등에도 활용)
ⓒ 순서 확인 : 특정 정점을 할 일이라고 본다면 그에 대한 연결을 통해 순서를 지정할 수 있다.(위상 정렬 예시)
ⓓ 연결성 확인 : 전자 회로 내 특정 회로가 상호 연결되어 있는지 확인하는 경우 등에 사용

이러한 문제들을 해결하는데 그래프를 어떻게 활용할 것인가? 이번 포스팅에서는 우선 그래프를 탐색하는 방법에 대해서 알아보자.

그래프 탐색에는 대표적으로 너비 우선 탐색(BFS, Breadth First Search), 깊이 우선 탐색(DFS, Depth First Search)가 있다. 여기서는 넓이 우선 탐색(BFS)을 알아보자.

너비 우선 탐색(BFS, Breadth First Search)

넓이 우선 탐색은 가장 쉽게 비교할 수 있는 것은 이전 포스팅의 트리(Tree) 구조의 계층 순회(Level Order) 이다. 트리 구조에서 계층 순회를 시작하면 각 계층의 모든 노드를 탐색한 뒤 그 아래 계층으로 넘어간다.

그래프도 동일한 방식으로 동작한다고 보면 되는데, 최초 시작 정점에서 가장 먼저 이어져 있는(간선으로 연결된) 정점을 모두 순회한 뒤, 각 순회된 정점부터 또 시작하여 가장 먼저 이어진 정점을 순회하는 방식을 반복한다.

트리와의 큰 차이점은, 그래프는 순환(Cycle)할 수 있다는 것이다. 그래서, 순환 탐지(Cycle Detection)를 할 수 있도록 추가적인 기능을 구현해야 한다는 것이다.

그림으로 보기

STEP 1: A노드 부터 탐색을 시작할 것입니다.

STEP 2: A노드를 Visited 리스트에 넣습니다. A노드에 인접한 B, C를 큐에 넣습니다.

STEP 3: 큐의 맨 앞에 있는 B를 Visited 리스트에 넣습니다. B에 인접한 노드 D를 큐에 넣습니다.

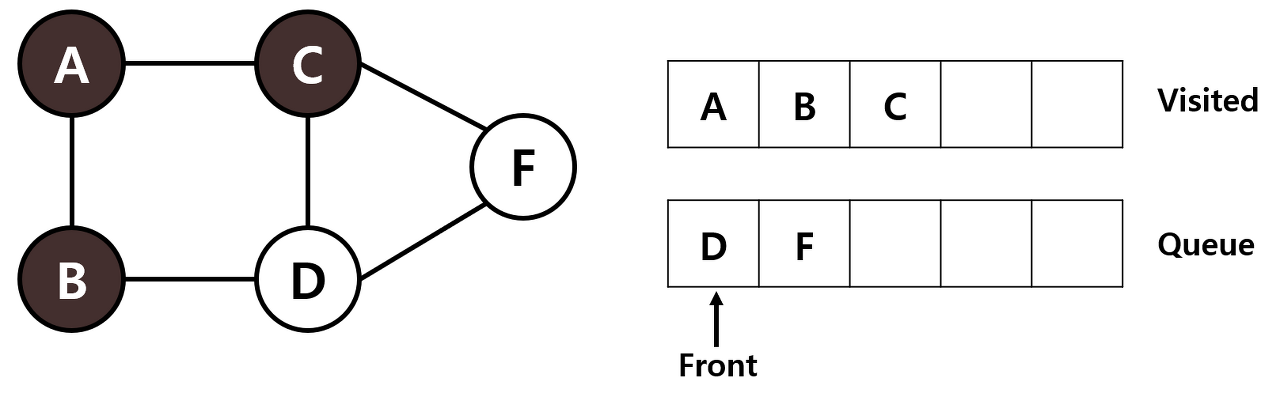
STEP 4: 큐의 맨 앞에 있는 C를 Visited 리스트에 넣습니다. C에 인접한 노드 F를 큐에 넣습니다.

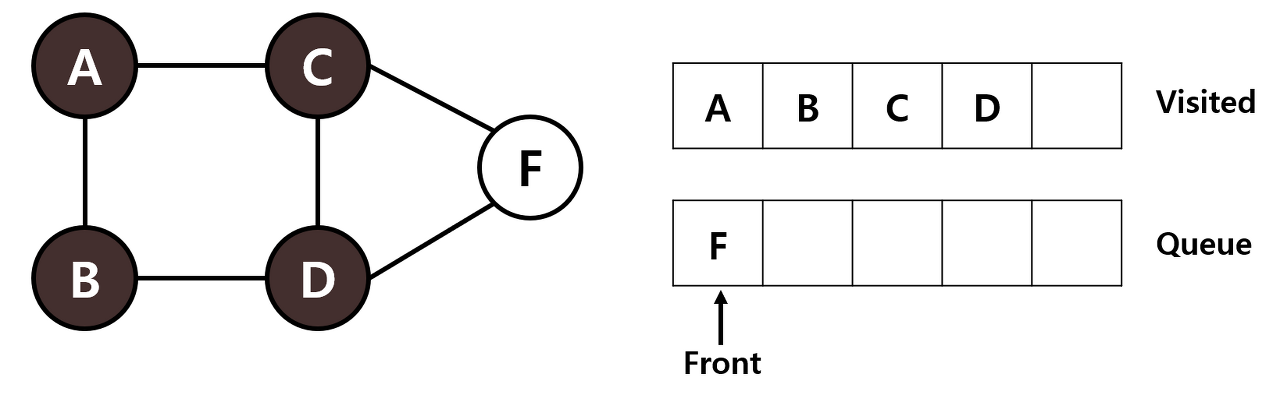
STEP 5: 큐의 맨 앞에 있는 D를 Visited 리스트에 넣습니다. D에 인접한 F는 이미 큐에 있으므로 넘어갑니다.

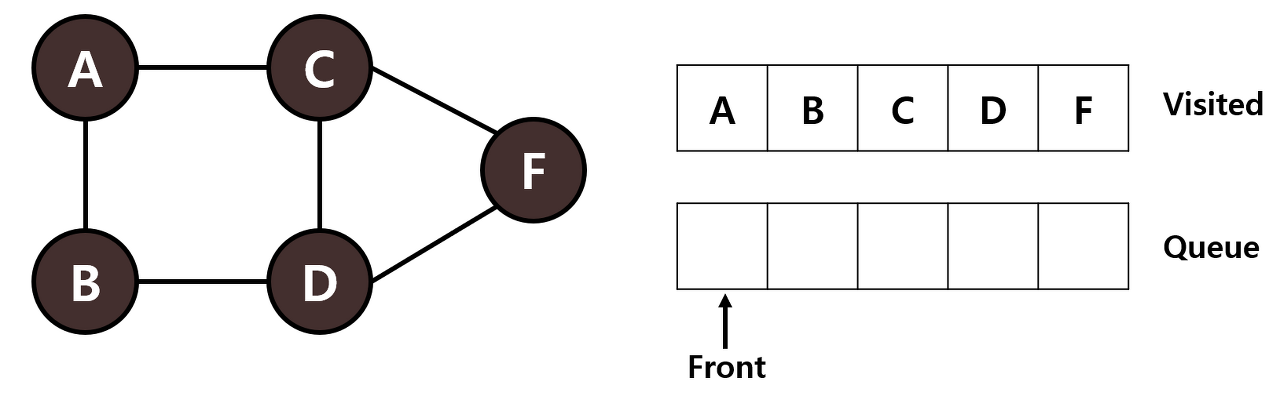
STEP 6: 큐의 맨 앞에 있는 F를 Visited 리스트에 넣습니다. 큐는 비어있게 되므로 탐색을 종료합니다.

BFS를 사용하는 예시

넓이 우선 탐색은 퍼즐 게임 등의 해결 시에 굉장히 많이 쓰일 수 있다. 루빅 큐브 등의 움직임을 해결할 수 있는 방식으로 활용 될 수 있다.

또한 굉장히 유명한 다익스트라(Dijkstra) 알고리즘으로 최단 경로를 찾을 때도 활용되며 Flow Network의 Maximum Flow를 찾기 위한 Ford-Fulkerson 알고리즘에도 사용된다. 이러한 내용은 추후 포스팅 진행.

최단 경로 문제

최단 경로 문제는 특히, DFS가 아닌 BFS로 풀어야 문제의 결과를 정확하게 나타낼 수 있다. 왜냐하면, BFS는 모든 정점의 방문 결과를 최단 경로로 보장이 가능하지만 DFS는 보장할 수 없기 때문이다.

하지만 모든 경우에 최단 경로 문제를 BFS로 풀 수 있는 것은 아니다. BFS로 최단 경로 문제를 해결 가능한 것은 가중치가 1일 때 만 가능하다. 1이 아니라면 다익스트라 또는 벨만 포드 알고리즘과 같이 응용하여 사용해야 한다.(추후 업데이트)

추가로, 그 가중치가 구하려는 문제의 답에 해당하는 것이어야 한다.(최단 거리면 거리가 가중치, 최단 시간이면 시간이 가중치여야 함!)
또한, 정점과 간선의 수가 너무 많으면 안된다.(O(V+E) 이기 때문에 보통 E가 V보다 많은데 E가 너무 많으면 시간 내에 해결이 불가함)

아래 예시를 보자.

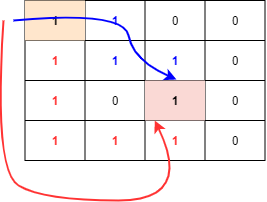
만약 우리가 주황색으로 칠해진 곳에서 빨간색으로 칠해진 곳으로 가고자 한다고 할 때, 유일한 경로는 파란 화살표와 빨간 화살표가 있을 수 있다.(다른 것도 가능하지만 대표적으로)

그럼 BFS로 탐색을 하면 빨간 부분, 파란 부분 인접 정점을 동시에 차례 대로 탐색을 하게 되며 시작점이 고정이라서 무조건 모든 인접 정점이 최소의 경우로만 이동하도록 보장이 된다.

그래서 BFS로 탐색 시, 원하는 위치에 도달했다면 추가 탐색을 그만두어 빠르게 문제를 해결할 수 있게 된다.

그런데 DFS로 탐색을 하면, 상단의 빨간색 부분 부터 우선 탐색이 이루어질 수 있다. 하지만 이 경로는 최소 경로라는 보장이 불가능하다! 실제 위의 예시에서는 최소 경로가 아니다.

보장을 하기 위해서는 이미 방문한 경로의 정점을 미 방문 상태로 전환하고 다른 모든 동일 위치에 도달할 수 있는 경우를 체크해야 하는데, 그것은 DFS가 아니라 Brute Force 방법이 된다. 그러면 문제를 푸는데, 시간복잡도가 높아져 문제를 풀 수 없게 된다.

(DFS, BFS는 기본적으로 이미 방문한 정점을 다시 방문하지 않아야 함!)

BFS 장단점

⭕ BFS 장점

답이 되는 경로가 여러 개인 경우에도 최단경로임을 보장한다.
최단 경로가 존재하면 깊이가 무한정 깊어진다고 해도 답을 찾을 수 있다.

❌ BFS 단점

경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.

구현 방법

create a queue Q 
mark v as visited and put v into Q 
while Q is non-empty 
    remove the head u of Q 
    mark and enqueue all (unvisited) neighbours of u

큐(Queue) 자료구조를 통해 구현된다. ( 큐 없이 인접 행렬을 통해 구현도 가능 여기 참조)

왜? 큐를 사용할까? 큐는 FIFO(First-In First-Out) 방식이다. 만약 내가 A 정점을 방문했고 B, C 정점이 인접 정점이라면 B, C를 모두 탐색한 뒤 B, C를 차례로 현재 정점으로 인식하여 다음 정점으로 이동해야 한다.

즉, A정점을 방문 시에, 다음으로 이동할 정점을 큐에 저장하여 First-things-First 라는 Fairness를 구현하고자 함이다.

스택(Stack)을 쓰면 안될까? 스택을 쓰게 되면 FILO(First-In Last-Out)이 되기 때문에 가장 인접한 정점이 가장 나중에 탐색되게 된다. 즉, 먼저 탐색되어야 할 노드가 나중에 탐색되어 First-things-First 탐색 원칙을 거스르게 된다. 그래서 이 방식은 이후 포스팅할 DFS(Depth First Search) 방식에서 활용 가능하다.

시간복잡도 : O(V+E), V는 정점 / E는 간선의 개수로 그 개수에 따라 전체 탐색에 시간이 소요된다.(인접 행렬은 O(V^2))

공간복잡도 : O(W), W는 Width로 너비의 크기를 말한다. 즉, 현재 정점의 인접 정점이 많으면 그만큼 큰 공간 복잡도를 갖는다.

코드

아래와 같이 구현할 수 있다. 주석 내용을 확인하며 코드를 이해하면 쉽게 이해할 수 있다.

여기서는 인접 리스트로 그래프를 구현했으며, Vertex 클래스를 별도로 만들어 인접리스트를 만들었다. 그래프 구현은 필요에 따라 상황에 맞게 수행한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

public class Graph {
 
    public static void main(String[] args) {
        Vertex v1 = new Vertex('A');
        Vertex v2 = new Vertex('B');
        Vertex v3 = new Vertex('C');
        Vertex v4 = new Vertex('D');
        Vertex v5 = new Vertex('E');
        Vertex v6 = new Vertex('F');
        Vertex v7 = new Vertex('G');
        Vertex v8 = new Vertex('H');
 
        Graph graph = new Graph(8);
        graph.addEdge(v1, v2); // A - B 연결
        graph.addEdge(v1, v3); // A - C 연결
        graph.addEdge(v2, v4); // B - D 연결
        graph.addEdge(v2, v5); // B - E 연결
        graph.addEdge(v3, v6); // C - F 연결
        graph.addEdge(v3, v7); // C - G 연결
        graph.addEdge(v5, v6); // E - F 연결
        graph.addEdge(v5, v8); // E - H 연결
        graph.addEdge(v6, v7); // F - G 연결
 
        graph.bfs(v1);
    }
 
    // 정점 데이터를 저장하는 클래스
    private static class Vertex{
        char data; //현재 정점의 데이터
        boolean visited = false; // 현재 정점을 이미 방문했는지 확인(Cycle방지)
 
        // 현재 정점의 인접 정점 리스트
        LinkedList<Vertex> adList = new LinkedList<>();
 
        Vertex(char data){
            this.data = data;
        }
    }
 
    private int v; // 정점의 개수
 
    public Graph(int v){
        this.v = v;
    }
 
    // Source 정점에서 Dest 정점을 이어주는 메소드
    // 상호 연결을 수행해줌.
    public void addEdge(Vertex v1, Vertex v2){
        v1.adList.addLast(v2);
        v2.adList.addLast(v1);
    }
 
    // BFS 시작하는 메소드
    // 탐색 시작할 Vertax를 parameter로 전달
 
    public void bfs(Vertex start){
        Queue<Vertex> queue = new LinkedList<>();
        queue.add(start); // 시작 정점 큐에 추가
        start.visited = true; // 시작 정점을 우선 탐색 완료 처리
 
        StringBuilder builder = new StringBuilder();
        // 더 이상 탐색할 정점이 없기 전까지 계속 반복 수행
 
        while(!queue.isEmpty()){
            Vertex cur = queue.poll();
            builder.append(cur.data).append(" ");
 
            // 현재 방문이 완료된 정점이 아니라면 다음 방문에 추가!
            for(Vertex v : cur.adList){
                if (!v.visited) {
                    queue.add(v);
                    v.visited = true; // 방문 완료 처리
                }
            }
        }
 
        System.out.println(builder.toString());
    }
}
Colored by Color Scripter

cs