[Softmax Regression] Softmax classifier 의 cost함수

[TensorFlow] Lab-05-2 Logistic Regression 모두의 딥러닝 시즌 2 정리...

복습...

지난 포스팅에서 우리는 오른쪽의 도식화된 것처럼 각각의 classifier을 이용해 계산하는 것보다 하나의 큰 Weight matrix를 갖고 계산하는 것이 더 편리하고 각각의

classifier의 결과 값을 갖는 하나의 벡터로 결과가 나오게 된다고 하였다.

이를 간단하게 도식화해보면 다음과 같다.

이때 \(Y_{A}\), \(Y_{B}\), \(Y_{C}\) 각각에 해당하는 실수 값들로 결과가 반환되었다.

하지만 우리가 원하는 바는 실수 값인 결과가 아닌 sigmoid 같은 것을 사용하여 0~1 사이의 값들로 반환되기를 원하였다.

이를 그림을 통해 간단하게 정리하면서 다음과 같다.

Sigmoid?

우리가 Logistic을 사용하여 WX = Y와 같이 벡터 계산을 하면 A, B, C에 대한 각각의 값 [2.0 1.0 0.1]이 나온다. 하지만 우리가 원하는 값은 P 값처럼 0~1 사이의 값들을 원했다.

또한 이때 우리는 실수 값들을 0~1 사이의 값들로 변환해 주면서 P 값들의 총합이 1이 되기를 원할 수도 있다. 이러한 형태로 표현하면 우리는 각각의 값을 확률처럼 이용할 수 있다.
확률처럼 이용할 수 있다는 것은 추후 우리가 분류를 할때 더 편하게 사용할 수 있기 때문에 우리는 각각의 값이 0~1 사이의 값을 가지고 그들의 합이 1이 되도록 하려고 한다.

그리고 이를 만족시켜주는 것이 바로 Softmax이다!!

Softmax function

softmax의 역할은 위의 그림과 같다. 실수 값이 입력되면

① 0~1 사이의 값으로 변환

② 모든 값들의 합이 1 ... 이는 각각의 값들을 확률로 볼 수 있다는 것이다.

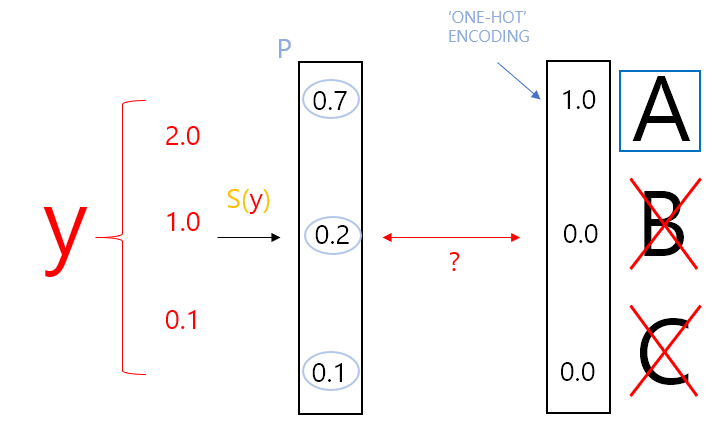
그리고 위의 그림처럼, 각각의 확률 값들 중 제일 큰 값을 1로 만들고 나머지를 0으로 만드는 One-Hot Encoding을 이용하여 특정 값만을 고를 수가 있다. 이는 텐서플로우에서 max 등의 함수를 이용하면 쉽게 구현할 수 있다.

여기까지 우리는 Hypothesis. 즉 예측하는 모델 완성을 하였다. 그리고 이제 우리가 해야 할 일은 예측한 값과 실제 값이 얼마만큼의 차가 존재하는지 나타내는

cost function을 설계해야 한다. 그리고 최종적으로 이 cost function을 최소화 함으로써 우리의 학습을 완성시키면 되는 것이다.

Cost function

이제 cost function에 대해 살펴보겠다. 일단 대략적인 동작을 살펴보고 자세한 얘기를 하고자 한다.

여기서 우리가 사용할 cost function은 바로 CROSS-ENTROPY이다.

L은 label. 즉 정답, Y, 실제 값이라고 한다.

S(y) 은hypothesis, 즉 우리가 softmax 함수를 이용하여 예측해낸 값으로 y hat이라고 하였다.

그리고 이 둘 사이의 차이가 얼마나 되는지를 계산하는 것이 위에 보이는 수식 cross-entropy이다.

Cross-entropy cost function

이제 이 cross-entropy가 어떻게 동작하는지. 왜 이 함수가 이 상황에서 적합한지에 대해 알아보겠다.

일단 위에서 보인 cross-entropy 수식을 살펴보자. 위에서 보인 수식은 다음과 같다.

그리고 이 수식의 \(S_{i}\)는 우리가 예측한 예측 값이고 -(마이너스)의 위치를 바꿔보면 아래와 같이 변형이 가능하다.

또한 아래에 보이는 -log의 경우 logistic regression에서 다룬 바가 있다.

s-y-130.tistory.com/27 _ 해당 포스팅 참고

이제는 해당 수식이 동작하는 것을 예시를 통해 알아보겠다.

아래 그림에서 예측 1의 경우 예측 값이 B로 실제 값을 잘 예측해서 ok.

예측 2의 경우 A를 예측해서 X를 판별받았다.

그리고 cost function이란 것은 예측이 맞을 경우에는 결과 값을 작게 반환하고 예측이 틀린 경우에는 터무니없이 큰 값을 반환하여 시스템에 벌?을 주는 것이다.

이젠 수식을 통해 실제로 벌?을 주는가에 대해 알아보자. 우선 수식을 살펴보면 \(L_{i}\), \(Y hat_{i}\)이 각 element로 수식을 다룬다는 것을 알수 있다.

예측 1의 오른쪽 행렬 계산을 살펴보면 실제 값에 -log(예측1). 즉 두 행렬을 원소끼리(element-wise) 곱하는 연산을 하고 있다. (이때의 element-wise를 ⊙로 표현)

그리고 예측 1의 각 요소를 -log에 대입하면 각각 [∞ 0]를 얻을 수 있고 이제 (실제 값 [0 1]) ⊙ (-log(예측1) [∞ 0])을 곱하면 [0 0]을 얻게 된다. 마지막으로 Σ가 있으므로 결과 값들의 총합을 구하면 0이 나오게 된다. 바로 이처럼 예측 1의 경우 예측을 잘했으므로 cost function은 매우 작은 값인 0을 반환함으로써 예측을 잘했다는 것을 알려주고 있다.

예측 2의 경우도 위에서처럼 계산을 진행하면 ∞을 반환하면서 터무니없는 결과 값을 반환하여 예측을 잘 못했다는 것을 알려주고 있다.

따라서 우리는 위의 예시를 통해 우리가 세운 Cost function은 올바른 것이라는 것을 증명하였다.

여러 개의 Training set이 있을 때는? 즉 N개의 전체 데이터에 대한 평균을 구한다고 하면??

N : 전체 데이터의 개수k : 클래스, feature의 개수

추가적으로 설명하자면 \(L_{j}\)는 \(S_{j}\)가 0 or 1인지 결정하는 요소라고 생각해봐도 될것이다. one-hot

전체의 D(Distance) or 차이를 구한 다음에 그것들을 합하고 전체의 평균을 내주면 된다.

이렇게 해주면 전체의 loss or cost function을 정의할 수 있다.

Logistic cost VS Cross entropy

그런데 이러한 Cost 함수는 우리가 지난 포스팅에서 알아보았던 Logistic cost 함수와 동일하다.

C, D는 각각 예측과 실제 값을 다룬다는 점에서 같다고 볼 수 있다. 그렇다면 두 수식은 왜 같은 것일까?

(강의에선 이 부분은 알아서 생각해보라고는 했다...)

일단 multinomial classification이 결국엔 logistic classifer로 구현이 가능하다는 점에 초점을 맞춰보고자 한다.

logistic classifer은 0, 1로 단 2개로 분류하는 알고리즘이다. 그리고 여러 개의 클래스를 구분하는 multinomial classification의 경우에도 아무리 작아도 최소 2개를 비교한다고 말할 수 있을 것이다.

이 둘의 차이점은 Cross entropy 에서는 A or B로 [1,0] or [0,1] 로서 서로 구분을 하는 거지만, Logistic 은 정답이 A라고 했을 때 이게 맞냐 아니냐 , 혹은, B라고 했을 때 이게 맞냐 아니냐를 판단하는 것이다.

그렇다면 이 둘의 공통점은?

공통점은 바로 서로 반대의 값만을 지닐수 밖에 없다는 것이다. 즉, 실제 값 \(L_{1}\), \(L_{2}\)은 1과 0, 그리고 서로 반대의 값을 지닐수밖에 없기 때문에 \(L_{2}\) = 1 - \(L_{1}\) 일 수밖에 없다.(0 또는 1, 1또는 0)

그리고 \(S_{1}\), \(S_{2}\)은 예측값이기 때문에 1, 0으로 딱 나오는 것이 아닌 0.3, 0.7 등으로 나오지만 결국 이 둘의 합은 1이 될 수밖에 없다.

이제 이 공통점을 수식에 적용하면 다음과 같을 것이다.

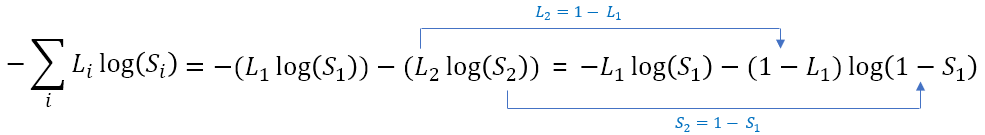
그리고 이제 \(L_{1}\) = y, \(S_{1}\) = H(x) 로 바꾸면 -ylog(H(x))-(1-y)log(1-H(x))가 되는 것이다.

이제 마지막 단계만 진행하면 끝이다!!

Gradient descent

위에서 처럼 cost function이 주어졌으면 이 cost를 최소화하는 값을 찾아내면 되는 것이다. 여기 같은 경우에는 W 벡터를 찾아내면 된다.

해당 알고리즘에 관한 내용은 이전 포스팅에서 다뤘으니 참고하기 바란다.

[Linear Regression] How to minimize cost

이제 해당 개념을 바탕으로 텐서플로우 라이브러리를 활용하여 구현해보도록 하겠다.

기본적인 Softmxa Classification

seyoung5744/Machine-learning-and-deep-learning-for-everyone

Contribute to seyoung5744/Machine-learning-and-deep-learning-for-everyone development by creating an account on GitHub.

github.com

간단한 동물 데이터를 활용한 Sotfmax Clssifier