![[Logistic Regression] Cost Function & Optimizer(Gradient Descent)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FIgeV9%2Fbtq2SMFOFxQ%2F9GAb67xnAJErod1YkiJisk%2Fimg.png)
[TensorFlow] Lab-05-2 Logistic Regression 모두의 딥러닝 시즌 2 정리...
전 포스팅에서 Logistic Function에 대한 개념을 정리하였다.
간단하게 정리.
- X라는 데이터가 주어졌을 때 linear regression을 통해 선형적인 값들을 도출할 수 있다.
- linear regression으로 도출한 linear한 값들은 Logistic function을 통해 0<=y<=1의 실수 값으로 만들어지게 된다.
- 이때 나온 실수값은 Decision Boundary를 통해 0, 1로 표현이 가능하다.
*위의 그림에서처럼 Y에 대한 표기를 나누기도 한다.
여기까지가 Logistic regression의 함수를 이용한 간략한 결과 도출방법이다.
이제는 위의 3단계를 토대로 학습을 위한 cost function.
그리고 이 학습에 대한 오차를 줄이기 위한 Optimizer에 대한 설명을 진행하겠다.
Cost Function
the cost function to fit the parameters(θ)
[Linear regression에서의 cost function]
linear regression에서 우리의 가설과 실제 데이터의 차이를 최소화하기 위한 최적의 W, b 값을 찾는 작업을 하였다.
이때 우리는 θ인 Weight값을 처음엔 랜덤하게 만들어 줬고 그리고 이 θ를 통해 만들어진 랜덤한 모델 값을 최적의 parameter로 만들어 주는것이 cost function의 역할이였다.
[logistic regression에서의 cost function]
그림으로 설명하자면 최초의 우리의 모델이 a라고 하자. 하지만 실제 우리가 원하는 모델은 b이다.
그럼 실제 우리가 원하는 모델(b)와 모델(a) 사이에 차이가 발생하는데 이 값을 바로 cost or loss라고 한다.
여기서 우리가 할 작업은 이 cost를 점점 줄임으로써 우리가 원하는 방향으로 즉, 모델a를 모델b로 만드는 것이다.
즉, 우리는 train set이 주어졌을 때 이를 통해 학습을 진행하는데 이때 학습된 결과로 최적의 parameter 모델을 찾는 것이 목표이다.
그리고 이 학습된 모델(hypothesis)에 새로운 데이터를 대입했을 시 나온 결과가 실제값(y)과 잘 들어 맞는다는 것은 cost가 0이라고 할수 있다.
아래 수식은 Logistic Regression에서의 cost function이다.
위의 수식자체를 TensorFlow Code로 나타내면 아래와 같다.
loss_fn의 인자 값으로 가설(hypothesis)과 실제 데이터(labels)을 넣어 우리가 원하는 cost 값을 return 받는 형식이다.
cost에 대해 좀더 자세히 설명해보겠다.
A convex logsitic regression cost function
(b)의 경우 모델이 ▲, ■ 을 정확하게 구분하고 있는데 이때의 cost는 0이라고 할 수 있다.
이에 반해 (a)의 경우 실제 우리가 원하는 모델과 차이가 발생하게 되고 이와 같을 때는 cost 값 자체가 크다는 것을 위의 그래프를 통해 확인할 수 있다.
위의 경우를 좀더 세밀하게 살펴보면 우리가 원하는 cost 값을 최소화하기 위한 과정은 실제 가설을 통해 나온 값에서 실제 label 값의 차이가 가장 최소화 되어야 한다.
우리는 logistic regression에서 cost function을 구할 때 실제 가설을 통해서 나오는 값이 sigmoid function과 같은 0, 1 사이의 실수값이 나왔다. (a-우리의 가설)
그에 반해 실제 우리가 원하는 값은 0, 1로 딱 떨어지는 값을 원했다. (b-0,1)
그리고 \(h_{θ}(x^i)\) - \(y_i\)와 비교해 (a) - (b)를 진행하면 (c)와 같은 값들이 나오게 된다. 이를 그래프로 나타내면 위의 (그림)_cost function 그래프와 같이 나타나게 된다.
그럼 이와 같은 함수를 실제 우리가 원하는 logistic regression cost function을 구하기 위해서는 Convex한 구조를 가져야 하는데...Convex하다는 것은 위의 그래프처럼 꼬불꼬불한 그래프가 아닌 ∩와 같은 볼록한 구조를 가져야만 실제 원하는 최적의 값을 구할 수 있게 된다.
여기서 그 전 포스팅에서 설명한 log 함수에 대한 추가 설명이 필요하다.
실제 로그 함수는 다음과 같이 나타난다.
위의 로그 함수를 살펴보면 1일 때는 0.
0으로 다가갈수록 -∞의 값을 가지게 되는데 이를 우리가 원하는 가설과 실제 값 차이.
이 차이를 두 가지 값으로 표현할 수 있다. => 0, 1
먼저 y = 1일때
우리가 가설을 통해 나온 값(\(h_{θ}(x)\))은 꼬불꼬불한 그래프의 값들 이였다. 그리고 이 값들을 로그에 대입하고 -를 붙이면 로그 함수는 다음과 같이 나타난다.
이제 위 그래프를 이용해 cost function을 나타낼 수 있다. 위 그래프를 살펴보면 우리가 원하는 값이 1(y=1)이고 실제
-log(h_θ (x))를 통해 나온 값도 1이면 당연히 cost의 값은 0으로 -log(h_θ (x)) 이 cost function에 성립이 된다.
이제 반해 값들이 0으로 갈 수록 cost가 점점 커지게 된다. 그럼 이제 우리는 -log(h_θ (x)) 수식을 통해 logistic regression의 1에 값에 대한 cost function을 구할 수 있다. (a)
y = 0일 때도 똑같은 방식으로 작동하게 된다. (b)
이렇게 얻은 (a) , (b)를 합치면 드디어 우리가 원하는 convex한 함수. 최적의 cost 함수를 얻을 수 있게 된다.
이를 TensorFlow code로 하면 아래와 같다.
Optimization
How to minimize the cost function
우리는 위에서 cost function을 이용하여 Convex한 구조로 각각의 cost 값을 구할 수 있는 함수를 찾아냈다.
그렇다면 우리는 우리가 찾아낸 cost function에 대해서 어떻게 cost 값을 최소화시킬 수 있을까?
이러한 minimize한 cost값을 찾아내는 과정을 바로 Optimization이라고 한다.
위의 그래프에서 각각의 지점에 Gradient가 존재한다. 그리고 이러한 Gradient 값을 최소화하는...이 경사 값을 0에 다다르게 하는 값을 구함으로써 우리는 우리가 원하는 cost 값을 0에 가깝게 만들어 낼 수 있다.
이제 이러한 과정을 수식으로 보면 다음과 같다.
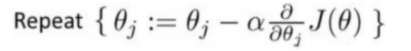
α : Learning rate
: Gradient...기울기(편미분)
J(θ) : Cost 값
위의 세 가지 값을 곱하고 업데이트함으로서 점점 목표를 향해 내려가는 수식이다.
3차원 공간에서 표현하면 다음과 같다.
시작 위치가 어디든간에 우리는 각각의 경사(기울기)를 통해서 점점 learning rate 만큼 내려가게 된다. 이렇게 학습을 하면서 계속 내려가게 되고 우리가 원하는 최적의 위치를 Optimization을 통해서 찾아내게 되는 것이다.
Optimization과정을 TensorFlow 코드로 나타내면 다음과 같다.
Summary
우리는 처음에 Logistic Regression을 이해하기 위해 다음과 같은 예시를 제시했다.
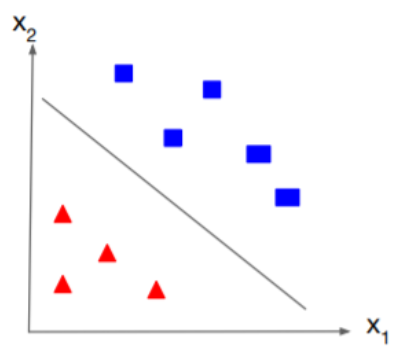
다음과 같은 데이터가 있을 때 어떻게 0, 1로 잘 구분하는 최적의 모델을 찾기 위한 cost function에 대한 이해를 진행했다.
또한 X 데이터가 있을 때 linear한 값을 얻고 이를 sigmoid function으로 0<=y=<1 사이의 값으로 만들었으며
Decision Boundary를 통해 0, 1 이 두가지 값으로 구분을 하였다.
이러한 하나의 일련의 과정은 뒤에서 설명할 Neural Network를 만들기 위한 하나의 컴포넌트라고 할 수 있다.
\(x_{0}\)라는 값이 들어갔을 때 \(w_{0}\)을 통해서 \(w_{0}\)\(x_{0}\)이런 Linear한 값(N)을 얻을 수 있으며 이렇게 얻은 N은 activation function이란 함수를 통해서 우리가 원하는 0, 1의 값을 구할 수 있게 된다.
이제 해당 개념을 바탕으로 텐서플로우 라이브러리를 활용하여 구현해보도록 하겠다.