탐욕법(Greedy Algorithm)

이것이 코딩 테스트다 with 파이썬 정리 및 추가 내용

Greedy Algorithm이란?

그리디 알고리즘(욕심쟁이 알고리즘, Greedy Algorithm)이란 "매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하자"라는 모토를 가지는 알고리즘 설계 기법이다.

예를 들어 5개의 도시를 모두 한번씩만 거쳐서 여행하는 경로 중 기름값을 아끼기 위해 가능하면 짧은 경로를 이용하고 싶다고 가정하자. 이 문제를 해결하기 위해 몇 가지 전략을 사용할 수 있다. 가능한 120가지의 조합을 모두 살펴봐서 그중 가장 짧은 경로를 선택하는 것도 하나의 전략이 될 것이다. 그러한 다양한 방법 중, 그리디 알고리즘을 사용한다는 것은 "지금 내가 있는 도시에서 고를 수 있는 도로 중 가장 짧은 도로를 선택한다"라는 방법이 될 수 있다.

(즉, 기준에 따라 좋은 것을 선택하는 알고리즘. 위의 예시에선 짧은 도로라는 기준이 주어진다.)

단, 그리디 알고리즘을 사용하면 매 선택이 그 순간에 대해서는 최적이지만 그걸 종합적으로 봤을 땐 최적이라는 보장은 절대 없다는 것을 명심해야 한다. 위의 예시에서 매 순간 최적을 따라가면 1-1-1-100라는 순서로 가는데, 중간에 1-1-10-10으로 움직이는 것이 전체적으로 더 짧은 길이 될 수 있다.

그리디 알고리즘을 한마디로 설명한다면 그 유명한 마시멜로 실험에 비유할 수 있겠다. 그리디 알고리즘을 사용한다는 것은 지금 당장 눈 앞에 있는 마시멜로를 먹는 것이다. 하지만 이 방법을 사용하는 것은 "기다렸다가 2개를 먹는다"라는 최적해를 보장해주지 못한다.

그리디 알고리즘은 부분의 최적해들의 집합이 곧 전체 문제의 해답이 될 때 사용할 수 있다. 위 서술 같은 경우는 그리디 알고리즘으로 해결할 수 없는 문제에 그리디 알고리즘을 적용한 경오니 당연히 최적해를 보장해주지 못한다.

(참고)
코딩 테스트에서 만나게 될 그리디 알고리즘의 문제 유형은 "사전에 외우고 있지 않아도 풀 수 있을 가능성이 높은 문제 유형"이라는 특징이 있다. 반면 이후 공부하게 될 정렬, 최단 경로 등의 알고리즘 유형은 이미 그 알고리즘의 사용 방법을 정확히 알고 있어야만 해결 가능한 경우가 많다.

* 참고로 다익스트라 알고리즘은 엄밀히 말하면 그리디 알고리즘으로 분류된다. 그리디 알고리즘이면서도 '암기'가 필요한 알로리즘이기도 하다.

이외에도 그리디 알고리즘 유형의 문제는 매우 다양하기 때문에 암기한다고 해서 항상 잘 풀 수 있는 알고리즘 유형이 아니다.
보통 코테에서 출제되는 Greedy Algorithm 유형의 문제는 창의력, 즉 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구한다.

어떤 경우에 잘 동작하는가?

그리디 알고리즘은

탐욕 선택 속성(greedy choice property)
- 탐욕적 선택 속성(greedy choice property) 은 동적 계획법처럼 답의 모든 부분을 고려하지 않고 탐욕적으로만 선택하더라도 최적해를 구할 수 있다는 것을 의미한다.
  즉, 앞에서 탐욕적인 선택을 해서 "손해"를 볼 일이 없어야 한다.
최적 부분 구조(optimal substructure)
- 최적 부분 구조(optimal substructure)는 탐욕적으로 선택한 매 순간의 결과가 전체 문제의 최적이어야 한다.만약 눈앞에 보이는 빠른 길만을 이용해 도착점에 도달했는데, 시작점에서 도착점으로 바로 가는 지름길이 더 빠른경우 탐욕적으로 선택하면 안된다는 것이다.

특성을 가지는 문제들을 해결하는데 강점이 있다. 즉, 한 번의 선택이 다음 선택에는 전혀 무관한 값이어야 하며 매 순간의 최적해가 문제에 대한 최적해여야 한다는 의미이다.

최적 부분 구조

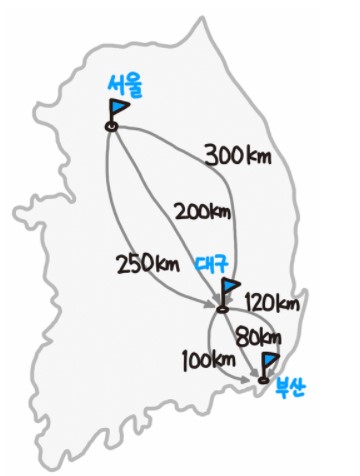
최적 부분 구조를 좀 더 살펴보면 그림과 같이 설명할 수 있다. 서울에서 부산까지 가는 최단 경로를 찾는다고 가정해보자. 그림에서 보듯이, 서울에서 대구까지 가는 경로는 3가지가 있으며, 부산까지도 마찬가지로 3가지 경로가 있다. 서울에서 부산까지 가는 최단 경로는 200km + 80km = 280km이다. 이 경로는 서울에서 대구까지 가는 최단 경로(200km)와 대구에서 부산까지 가는 최단 경로(80km)로 구성된다. 즉 서울에서 부산까지 가는 최단 경로는 각각의 부분 문제인 1) 서울에서 대구까지 가는 최단 경로 문제와 2) 대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합이다. 따라서 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성된다. 이러한 구조를 최적 부분 구조라 한다.

근사 알고리즘

상기했다시피 그리디 알고리즘은 100% 최적해를 보장해주지 않는다. 다만, 어느 정도 적합한 수준의 해답을 알려준다. 따라서, 최적이 아닌 "되는가" 또는 "적당히 괜찮은 방법"을 찾을 때에는 사용할 수 있다. 특히, 계산속도가 정확한 알고리즘에 비해서 빠른 경우가 많기 때문에 실용적으로 사용이 가능하다. 하나 이게 정말로 "적당히" 괜찮은지에 대해서 알려면 정확한 증명이 수반될 수 있다. 또한, 해답을 찾아가는 과정에 있어서 그리디로 구한 값을 비교 값으로 설정할 수가 있다.

사용되는 예시

AI에 있어서 결정 트리 학습법(Decision Tree Learning)
활동 선택 문제(Activity selection problem)
거스름돈 문제
최소 신장 트리 (Minimum spanning tree)
제약조건이 많은 대부분의 문제[1]
다익스트라 알고리즘
허프만 코드
크리스컬 알고리즘

[1] 항상 그런것은 아니지만, 프로그래밍 문제를 풀 때 제약조건이 많다면 대부분 그리디로 풀리는 경우가 많다. 다만 그리디인줄 알고 풀었다가 피보는 경우도 있다.

최적 값을 구하는 데 실패하는 문제들

외판원 순회 문제 (TSP, Traveling Salesperson Problem)
- 단, TSP와 같은 NP-Complete 문제를 풀기 위한 근사값을 추정하기 위해 사용하기도 한다.
배낭 문제 (Knapsack Problem)

Greedy Algorithm 대표 예시

이제 Greedy Algorithm이 대표 문제를 살펴보면서 감을 잡도록 하겠다.

보통 Greedy Algorithm은 '가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준을 알게 모르게 제시해준다. 대체로 이 기준은 정렬 알고리즘을 사용했을 때 만족시킬 수 있으므로 그리디 알고리즘 문제는 자주 정렬 알고리즘과 짝을 이뤄 출제된다.

또한 대표적으로, Minimum Spanning Tree 를 구하는 방법인 Prim Algorithm, Kruskal Algorithm이 있다.

그 외에도, 가중치가 있는 방향 그래프에서 최단거리를 구해주는 Dijkstra Algorithm, 거스름돈 나누기 등이 있다.

1. 거스름돈

당신은 음식점의 계산을 도와주는 점원이다. 카운터에서는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러 줘야 할 동전의 최소 개수를 구하라.

단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.

문제 해설

'가장 큰 화폐 단위부터' 존을 거슬러 준다.

n = 1260
count = 0

# 큰 단위의 화폐부터 차례대로 확인
list = [500,100,50,10] 

for coin in list:
    count += n // coin # 해당 화폐로 거슬러 줄 수 있는 동전의 개수 세기
    n %= coin
    
print(count)

코드를 보면 화폐의 종류만큼 반복을 수행해야 한다. 따라서 화폐의 종류가 K개라고 할 때 위 소스 코드의 시간 복잡도는 O(K)이다. 참고로 시간 복잡도에서 서슬러 줘야 할 돈 N은 찾아볼 수 없는 것을 알 수 있다. 즉, 이 알고리즘의 시간 복잡도는 동전의 총 종류에만 영향을 받고, 거슬러 줘야하는 금액의 크기와는 무관하다는 것을 알 수 있다.

그리디 알고리즘의 정당성

그리디 알고리즘은 모든 알고리즘 문제에 적용할 수 있는 것은 아니다. 대부분의 문제는 그리디 알고리즘을 이용했을 때 '최적의 해'를 찾을 수 없을 가능성이 다분하다. 하지만 거스름돈 문제에서 '가장 큰 화폐 단위부터' 돈을 거슬러 주는 것과 같이, 탐욕적으로 문제에 접근했을 때 정확한 답을 찾을 수 있다는 보장이 있을 때는 매우 효과적이고 직관적이다.

그리디 알고리즘으로 문제의 해법을 찾았을 때는 그 해법이 정당한지 검토해야 한다. 위 예시인 거스름돈 문제를 그리디 알고리즘으로 해결할 수 있는 이유는 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문이다.

실제로 우리가 문제를 풀 때에는 그리디를 생각해내기 쉽지 않고, 많은 경우 그리디로 풀면 되겠다! 싶은데

실제로 풀면 최적해를 찾지 못하여 틀리는 경우도 있고, 풀었으나 왜 이게 최적인지 확실하게 증명하지 못하는 경우가 많다.

따라서 적용하기 전 그리디 알고리즘의 정당성을 검증해 봐야 한다. (연습 필요!!)

그리디 알고리즘 풀이 순서

이 풀이 순서는 종만북에 쓰여있는 "탐욕적 알고리즘 레시피" 를 인용하였습니다.

문제의 답을 만드는 과정을 여러 조각으로 나눈다.
각 조각마다 어떤 우선순위로 선택을 내려야 할지 결정한다. 이에 대한 직관을 얻기 위해서는 예제 입력이나 그 외의 작은 입력을 손으로 몇 개 풀어보는 것을 추천
어떤 방식이 동작할 것 같으면 두 가지 조건을 증명해보자. (탐욕적 선택 속성, 최적 부분 구조)

2. Kruskal Algorithm

그래프의 모든 간선(edge)중에서 가중치가 가장 작은 것부터 차례대로 선택한다(단, Cycle을 만드는 경우는 제외)

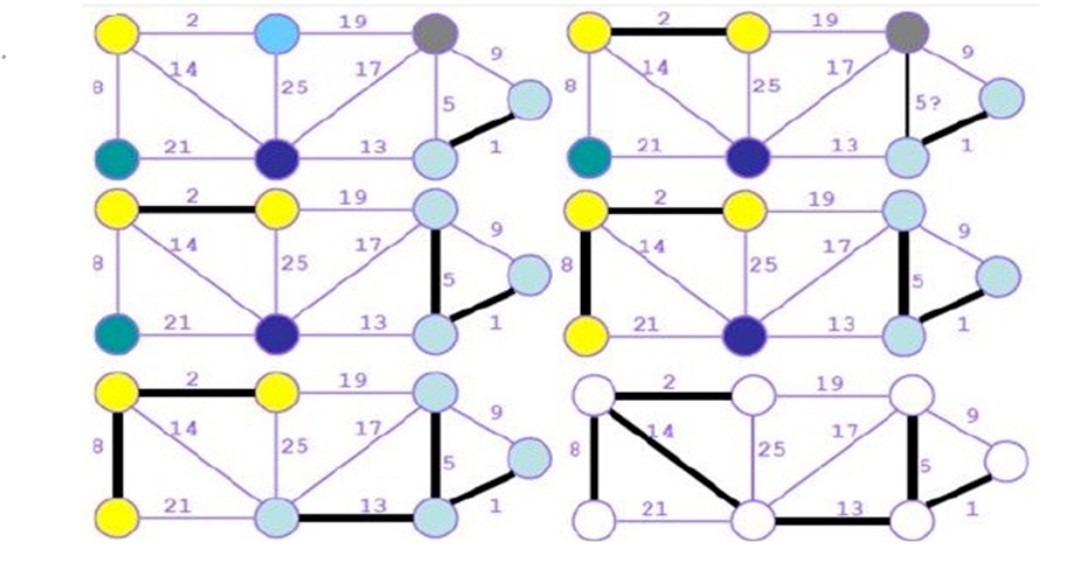
3. Prim Algorithm

임의의 정점(vertex)에서 가중치가 가장 작은 간선(edge)을 선택,

선택된 정점(vertex)와 연결된 간선(edge)들 중에 가장 가중치가 작은 것들을 선택(단, cycle을 만드는 경우는 제외)

4. Dijkstra Algorithm

가중치가 있는 방향그래프에서 임의의 두 노드 사이의 최단거리를 구하는 알고리즘.

참고

namu.wiki/w/%EA% B7% B8% EB% A6% AC% EB%94%94%20% EC%95% 8C% EA% B3% A0% EB% A6% AC% EC% A6%98#fn-3

https://ujink.tistory.com/10