![[Application & Tips] Overfitting](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fcw36vp%2Fbtq4eiYxUQX%2FglqFX1vlUKQ5JKBsFpl4JK%2Fimg.png)
[TensorFlow] Lab-05-2 Logistic Regression 모두의 딥러닝 시즌 2 정리...
목차
- Learning rate
- Gradient
- Good and Bad Learning rate
- Learning rate schedule 과 Annealing the learning rate (Decay)
- Data preprocessing
- Feature Scaling - Standardization / Normanalization
- Noisy Data
- Overfitting
- Set a Feature
- Regularization
overfitting에 관해 설명하기에 앞서 그래프를 통해 간단하게 설명하고 지나가겠다.
위의 그래프를 살펴보면 실제 우리가 모델을 만드는 과정에서는 Validation data set을 통해 평가를 하면서 학습을 진행한다. 그리고 정상적으로 학습이 잘 되었을 경우 높은 Accuracy를 나타내며 새로운 데이터인 Test 데이터를 갖고 평가를 해보면 Test data set에서도 높은 Accuracy를 보인다.
하지만 위의 Val 그래프는 학습을 하는 과정에서 우리가 사용한 데이터만으로 평가를 하다 보니 사용된 데이터에만 맞춰져서 모델이 만들어졌고 이때는 높은 Accuracy를 나타낸다. 그치만 새로운 데이터(Test)로 평가를 하게되면 오히려 Accuracy가 떨어지는 현상이 발생하는데 이를 바로 Overfitting이라고 한다.
Overfitting
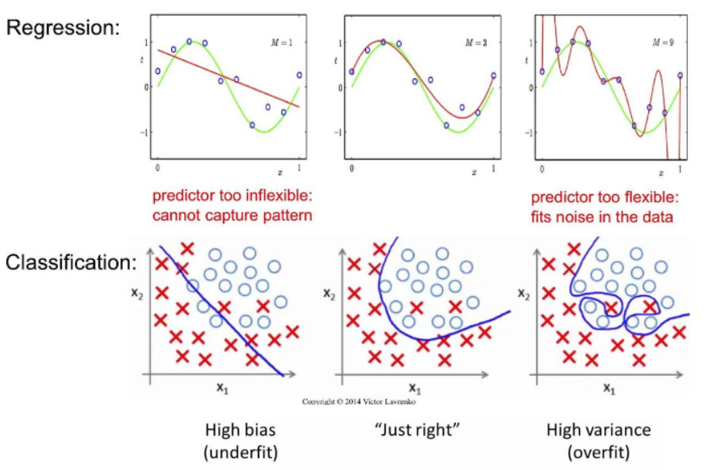
Linear, Logistic 각각에서의 overfitting
Overfitting은 학습데이터에 지나치게 맞는 모델을 학습함으로써 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말한다. 기계학습은 범용 성능을 진향한다. 하지만 학습 데이터은 포함되지 않는, 아직 보지 못한 데이터가 주어져도 바르게 식별해내는 모델이 바람직하다. 복잡하고 표현력이 높은 모델을 만들 수는 있지만, 그만큼 오버피팅을 억제하는 기술이 중요해지는 것이다.
그래서 일반적으로 학습이 진행됨에 따라 학습 데이터인 Trainig Dataset의 오차는 줄어들지만, 검증 데이터인 Validation Dataset의 오차는 감소하다가 일정 시점이 지나면 증가하게 된다. 보통 이 시점에서 학습을 멈추어 일반화된 모델을 생성하는 것이 좋다.
Overfitting 발생 원인
그렇다면 이런 overfitting이 발생하는 원인은 무엇일까?
- 학습 데이터는 실제 데이터의 부분 집합이라서 실제 데이터의 모든 특성을 가지고 있지 않을 수 있다.
- 데이터 편향 : 학습 데이터는 실제 데이터에서 편향된 부분만을 가지고 있을 수 있다.
- 데이터 오류 : 학습 데이터에는 오류가 포함된 값이 있을 수 있다.
- 과거 학습한 데이터가 대표성을 가지지 못하는 경우 발생할 수 있다.
- 고려하는 변수가 지나치게 많을 때 발생할 수 있다.
- 차원의 저주 현상, 데이터가 표현하는 공간이 넓어지면서 얕게 분포, 점들이 서로 멀어지면서 각 값들이 모델에 미치는 영향이 커짐, 즉 극단적인 값이 평균에 영향을 주게 된다.
- 모델이 너무 복잡한 경우 발생할 수 있다.
- 오류가 거의 0에 가까운 모델이라 할지라도 실제 눈으로 예측하는 관계와는 큰 차이가 발생할 수 있기 때문에 교차 타당성 검증을 수행해야 한다.
- 보통 훈련 집합을 이용하여 적합(fitting)을 하게 되는데 이때, 예측 모델이 훈련이 아주 잘 되었다고 하더라도 과적합(Overfitting) 문제가 발생한다.
아래는 overfitting, underfitting에 대한 간단한 원인 분석 표이다.
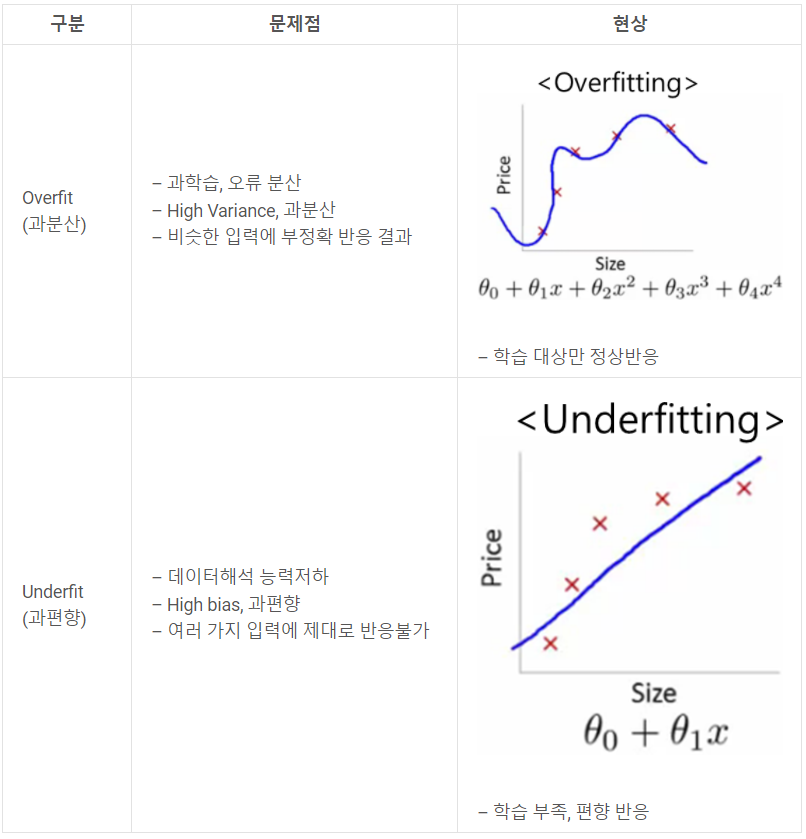
Overfitting 해결 방법
사실 Overfitting을 해결하는 방법은 애초에 Overfitting 발생을 방지하고 예방하는게 최고지 않을까?
가~장 이상적인 경우는 기본적으로 Validation Dataset 오차가 감소하다가 증가하는 시점에서 학습을 중단하면 된다.
하지만 이게 쉬우면 Overfitting을 해결하는 많은 방법들이 나왔을리가 없다고 생각했다...
Overfitting을 해결하기 어려운 이유
1. 학습 데이터는 실제 데이터의 부분 집합이고, 실제 데이터를 모두 수집하는 것은 불가능한 경우가 많다.
2. 실제 데이터를 모두 수집하더라고 모든 데이터를 학습시키는 것이 불가능한 경우가 많다.
3. 학습 데이터만으로는 실제 데이터와의 오차가 커지는 지점을 정확하게 알기 어렵다.
이것들이 Overfitting을 해결하는 방법들이다. (과적합(Overfitting)을 막는 방법들)
- Feature Normalization
- Regularization
- More Data and Data Augmentation
- Color Jiltering
- Horizontal Flips
- Random Crops/Scales
- Dropout (0.5 is common)
- Batch Normalization
하지만 난 일단은 이 중에서 몇가지만 우선적으로 정리하려고 한다.
Set a feature
우선 feature set에서 해결할 수 있는 방법으로는 다음 3가지이다.
- Get more training data - more data will actually make a difference, (helps to fix high variance)
- Smaller set of features - dimensionality reduction(PCA) (fixes high variance)
- 차원을 줄임으로 써 좀더 각각의 feature가 갖는 속성이 가진 의미를 좀 더 분명히 할수 있다.
- Add additional features - hypothesis is too simple, make hypothesis more specific (fixes high bias)
Regularization (Add term to loss)
위 그림에서도 알 수 있 듯, 만약 우리가 주어진 데이터에 비해서 높은 complexity를 가지는 model을 learning하게 된다면 overfitting이 일어날 확률이 높다. 그렇다면 한 가지 가설을 세울 수 있는데, ‘complexity가 높을 수록 별로 좋은 모델이 아니다.’ 라는 가설이다. 이는 Occam’s razor, 오컴의 면도날이라 하여 문제의 solution은 간단하면 간단할수록 좋다라는 가설과 일맥상통하는 내용이다.
하지만 그렇다고해서 너무 complexity가 낮은 model을 사용한다면 역시 부정확한 결과를 얻게 될 것은 거의 자명해보인다. 그렇기 때문에 우리는 원래 cost function에 complexity와 관련된 penalty term을 추가하여, 어느 정도 ‘적당한’ complexity를 찾을 수 있다. 이를 regularization이라 한다
정리하자면 Regularization은 '정규화'라고도 하면 보통 '일반화'라고 번역하는 것이 더 적합할 듯하다.
이 용어는 기계학습뿐만 아니라 통계에서도 흔히 사용되는 용어로 Regularization은 일종의 penalty 조건에 해당하는 것이다.
통상적으로 기계학습이나 통계적 추론을 할 때 cost function 혹은 error function이 작아지는 쪽으로 진행을 하게 된다.
단순하게 작아지는 쪽으로만 진행을 하다 보면, 특정 가충지 값들이 커지면서 오히려 결과를 나쁘게 하는 경우도 있다.
아래 그림은 regularization을 통해 더 좋은 학습 결과를 가져오는 경우를 보여주는 그림이다.
간단한 예시를 통해 설명을 해보자.
다음과 같이 Linear regression의 가설과 cost function이 있다고 하자.
그리고 θ를 각각 1, 2, 100, 3, 4 라고 해보자. 이렇게 되면 아무래도 θ = 100인 weight 값이 큰 영향을 미칠 수 밖에 없을 것이다. 그렇다면 우리는 여기서 위의 λ(람다)를 통한 '정규화'를 통해 모델에 weight의 평균값을 줌으로써 overfitting을 방지하는 것이다. (L2 Norm)
나름 강의와 추가적인 내용을 통해 정리는 해봤지만 더 좋은 포스팅도 많고 다른 관점의 좋은 글도 찾았다.
해당 두 포스팅을 꼭 읽어보길 바란다. 설명이 너무 좋은거 같다.
Regularization에는 L1, L2 regularization도 존재하고 정리해야 할 부분이 너무 많기 때문에 나중에 따로 정리해볼 생각이다.
mangkyu.tistory.com/37?category=767742
m.blog.naver.com/laonple/220527647084
이제 지금까지 배운 내용을 토대로 Tensorflow 코드를 작성해보자.
07-3-linear_regression_eager (preprocess, decay, l2_loss)
참고