해싱이란? (Hashing)
해싱이란 임의의 길이의 값을 해시함수(Hash Function)를 사용하여 고정된 크기의 값으로 변환하는 작업을 말한다.
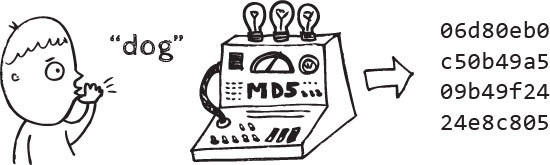
위 그림에서 dog 라는 문자열을 해시함수를 이용해 새로운 값으로 변환한 것을 볼 수 있는데 이 경우엔 암호화에 쓰이는 해시 알고리즘인 MD5를 사용한 것이다.
만약 특정 길이를 32bit로 고정된다고 가정하에 아주 간략하게 보자면 다음과 같은 이미지라고 보면 된다.

※ 참고
이 때 32bit는 2진수일 때 기준이므로, 16진수로 보자면 4bit당 한 묶음이기 때문에 16진수로 표현하면 8개의 문자를 얻게 될 것이다. 즉, 해시함수를 돌리기 전 문자열의 길이가 얼마건 일정한 길이를 얻는다는 것이다. 실제로 대표적인 해시함수인 SHA계열의 SHA-512는 512bit의 고정된길이를, SHA-256은 256bit의 고정된 길이로 매핑한다는 의미다.
이러한 과정을 '해싱(hashing)'한다고 하며, 해시함수에 얻어진 값을 보통 다이제스트(digest)라고 한다.
그러면, 왜 굳이 복잡하게 해시함수를 돌리는가? 라는 의문점이 있을 것이다.
우리가 그동안 학습했던 ArrayList, LinkedList 등 수많은 자료구조에서 '특정 값'이 있는지 찾아내기 위해서 어떻게 하였는가?
배열 혹은 노드를 순회해보면서 특정값이 있는지 찾아냈었어야 한다.
하지만 해시함수를 이용한다면 굳이 순회할 필요가 없다.
왜냐하면, 동일한 메세지(값)에 대해서는 동일한 다이제스트를 갖기 때문이다.
무슨말인가 하면, 위 이미지에서 a 문자열을 hash함수에 돌려 얻은 값이 86aff3ca 였다. 이는 고정된 값이다. 즉, 동일한 해시 알고리즘을 사용하는경우 동일한 값에 대하여 동일한 다이제스트를 얻게 된다는 것이다.
정말 그럴까?
테스트로 SHA256 에 123456 이라는 문자열을 입력했더니 이런 값이 나왔다.
8d969eef6ecad3c29a3a629280e686cf0c3f5d5a86aff3ca12020c923adc6c92이는 어느 사이트에서건, 혹은 프로그램을 통해 SHA256로 123456을 해보면 위와 똑같은 값을 얻을 것이다. (SHA3-256과는 다른 것이므로 주의)
즉, 특정 값에 대한 다이제스트는 변하지 않기 때문에 이 다이제스트의 값을 배열의 위치(index)로 활용하는 것이다. 좀 더 쉽게 말하자면 특정 값에 대해 배열의 특정 위치로 지정해두는 것과 같다고 보면 된다.
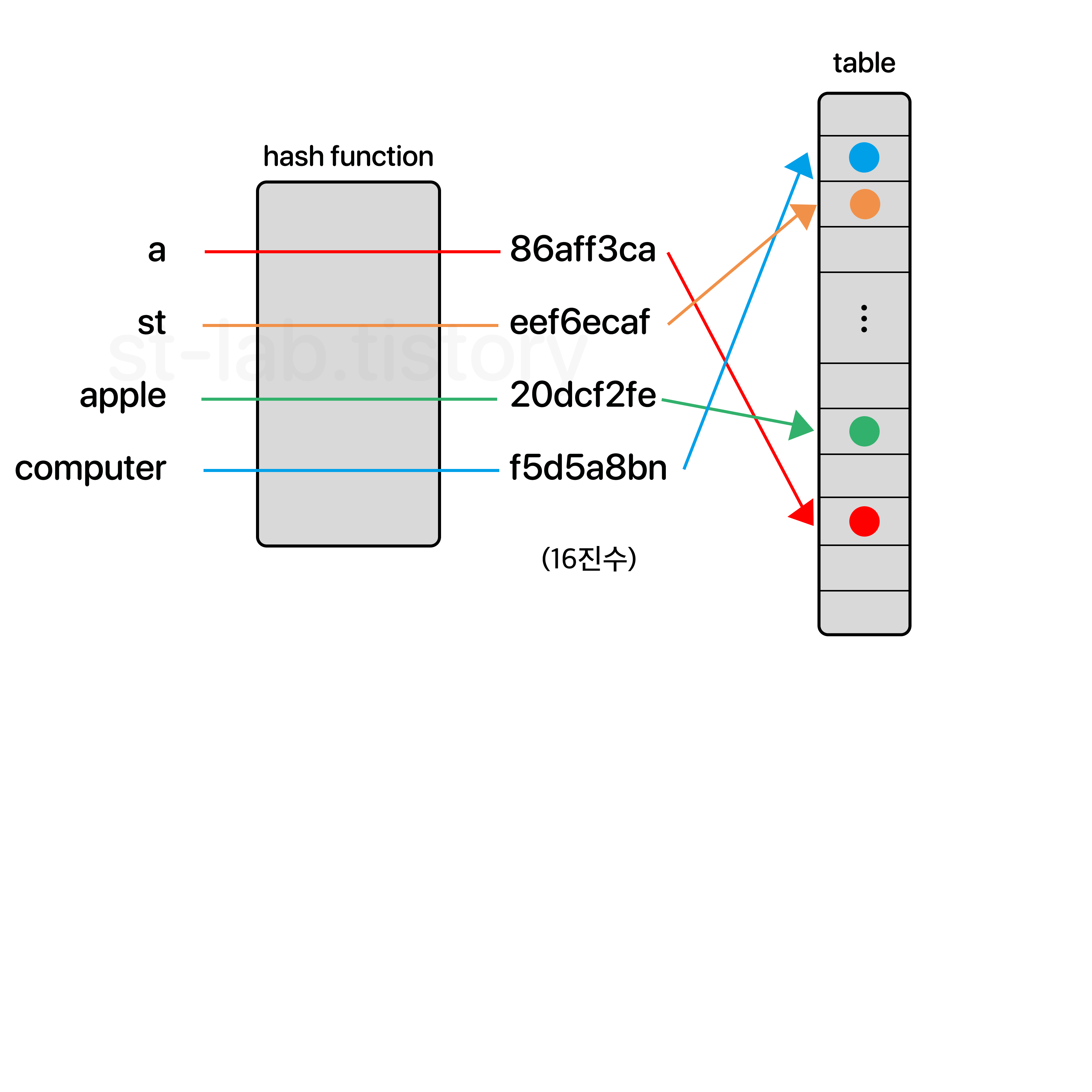
하지만 여기서 다룰 것은 암호화에 쓰인 방식이 아닌 자료구조로 사용하고자 하는 해시 테이블을 다루기 때문에 정수값으로 변환되는 해시 알고리즘을 사용한다. 해싱을 사용하여 데이터를 저장하는 자료구조를 해시 테이블(Hash Table)이라고 하며 이는 기존 자료구조인 이진탐색트리나 배열에 비해서 굉장히 빠른 속도로 탐색, 삽입, 삭제를 할 수 있기 때문에 컴퓨터 공학도라면 반드시 알아야 한다.
해시테이블(HashTable)이란?
해시 테이블이란 해시함수를 사용하여 변환한 값을 색인(index)으로 삼아 키(key)와 데이터(value)를 저장하는 자료구조를 말한다. 기본연산으로는 탐색(Search), 삽입(Insert), 삭제(Delete)가 있다.
1. Direct Address Table
먼저 가장 간단한 형태의 해시테이블로 이름 뜻대로 키 값을 주소로 사용하는 테이블을 말한다. 이는 키 값이 100이라고 했을 때 배열의 인덱스 100에 원하는 데이터를 저장하는 것이다.

위 그림에선 키 값이 21였기 때문에 인덱스 21에 원하는 데이터를 저장한 경우이다. 이러한 자료구조는 탐색, 삽입, 삭제 연산을 모두 에 할 수 있지만 다음과 같은 한계점이 있다.
- 최대 키 값에 대해 알고 있어야 한다.
- 최대 키 값이 작을 때 실용적으로 사용할 수 있다.
- 키 값들이 골고루 분포되어있지 않다면 메모리 낭비가 심할 수밖에 없다.
2. Hash Table
앞서 해시 테이블은 (Key, Value)로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있는 자료구조라고 하였다.
해시 테이블이 빠른 검색속도를 제공하는 이유는 내부적으로 배열(버킷)을 사용하여 데이터를 저장하기 때문이다.
해시 테이블은 각각의 Key값에 해시함수를 적용해 고유한 해시값을 생성하고, 이 해시값을 배열의 고유한 Index로 변화하여 값을 저장하거나 검색하게 된다.
여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.
- 버킷(bucket) : 버킷은 해시 테이블의 행 인덱스(주소)
- 슬롯(slot) : 슬롯은 그 행을 열의 인덱스(주소)
아래의 그림은 버킷이 11, 슬롯이 3인 해시 테이블이다. 여기서 data가 전부 차있는 버킷도 존재하고 그렇지 않은 곳도 존재한다. bucket[0]을 보면 이미 데이터가 가득차 있다. 만약 다음에 들어올 데이터가 bucket[0]에 들어갈 데이터라면 어떻게 될까? 넣을 수 없는 상황이 될것이다.
그것을 오버플로(Overflow) or 해시 충돌 이라고 하며 이 문제를 해결해야 한다. 잠시후 설명.

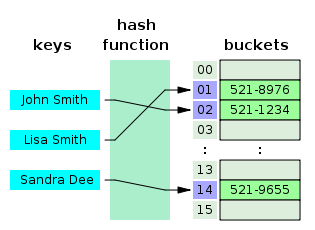
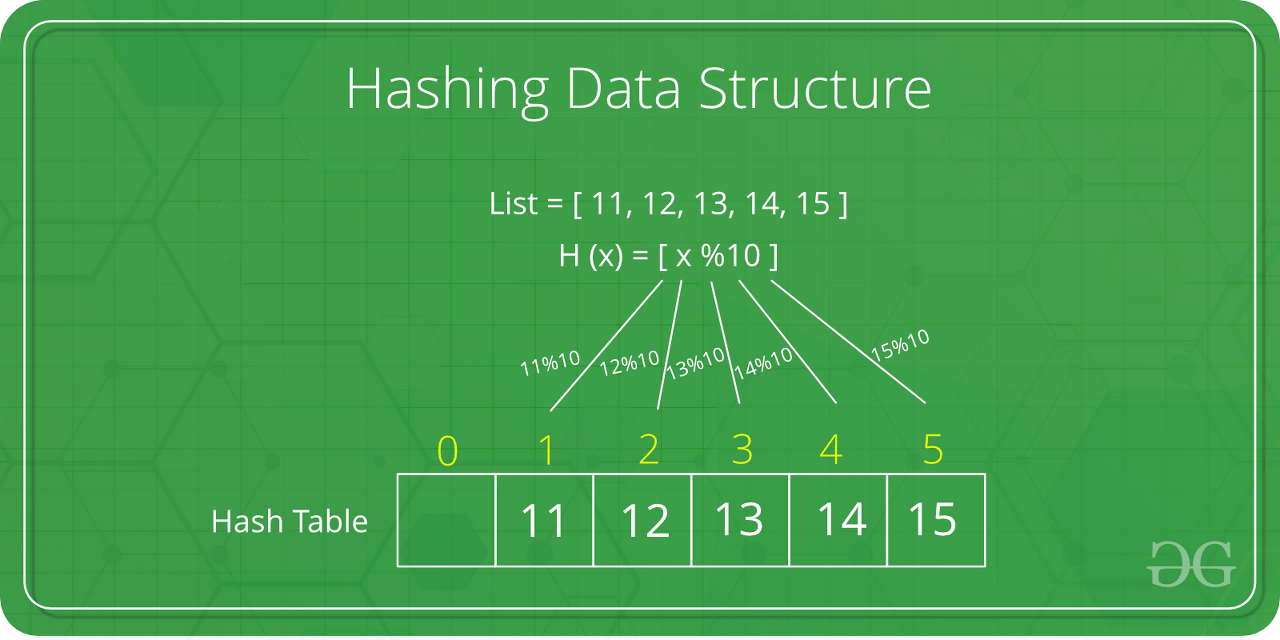
예를 들어 우리가 (Key, Value)가 ("John Smith", "521-1234")인 데이터를 크기가 16인 해시 테이블에 저장한다고 하자. 그러면 먼저 index = hash_function("John Smith") % 16 연산을 통해 index 값을 계산한다. 그리고 array[index] = "521-1234" 로 전화번호를 저장하게 된다.
이러한 해싱 구조로 데이터를 저장하면 Key값으로 데이터를 찾을 때 해시 함수를 1번만 수행하면 되므로 매우 빠르게 데이터를 저장/삭제/조회할 수 있다. 해시테이블의 평균 시간복잡도는 O(1)이다.
Hash 함수(해시 함수)
해시 함수에서 중요한 것은 고유한 인덱스 값을 설정하는 것이다. 해시 테이블에 사용되는 대표적인 해시 함수로는 아래의 4가지가 있다.
| 해시 함수 | 설명 |
| Division Method | 나눗셈을 이용하는 방법으로 입력값을 테이블의 크기로 나누어 계산한다. ( 주소 = 입력값 % 테이블의 크기) 테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 알려져 있다. |
| Digit Folding | 각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다. |
| Multiplication Method | 숫자로 된 Key값 K와 0과 1사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같은 계산을 해준다. h(k)=(kAmod1) × m |
| Univeral Hashing | 다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법이다. |
해시(Hash)값이 충돌하는 경우
앞서 해시 테이블을 얘기하며 개념자체가 어려운 것은 아니지만 문제가 되는 것은 충돌(Collision)이다. 충돌에 대해서 이해하기 위해선 먼저 적재율(Load Factor)에 대해서 이해해야 한다.
Constructs a new, empty set; the backing
HashMap
instance has default initial capacity (16) and load factor (0.75).
HashMap과 관련된 문서에는 위와 같이 적혀있는데 해석해보면 기본 초기 용량 = 16, 로드팩터 = 0.75라고 하는 것을 볼 수 있다.
Load Factor란 무엇인가?
적재율이란 해시 테이블의 크기 대비, 키의 개수를 말한다. 즉, 키의 개수를 , 해시 테이블의 크기를 이라고 했을 때 적재율은 이다.
데이터의 개수가 증가해서 Load Factor의 값이 원래 Load Factor의 값보다 커지게 되면 저장 공간의 크기는 증가되고 해시 재정리 작업(refresh)을 해야만 한다. Load Factor라는 값이 클수록 공간은 넉넉해지지만, 데이터를 찾는 시간은 증가한다.
따라서 초기 공간 개수와 Load Factor는 데이터의 크기를 고려하여 산정하는 것이 좋다. (즉, Load Factor는 데이터를 효율적으로 관리하기 위해서 처음에 설정하는 값이라고 생각하면 된다.)
그리고 데이터가 어느정도 쌓이면 버킷 사이즈를 resized 해야할 지에 대한 기준이라고 생각할 수 있다
왜냐하면 초기크기가 (데이터의 개수)/(Load Factor) 보다 클 경우에는 데이터를 쉽게 찾기 위한 해시 재정리 작업이 발생하지 않기 때문이다. 따라서 대량의 데이터를 여기에 담아 처리할 때에는 초기 크기와 Load Factor의 값을 조절해 가면서 가장 적당한 크기를 찾아야만 한다.
Direct Address Table은 키 값을 인덱스로 사용하는 구조이기 때문에 적재율이 1 이하이며 적재율이 1 초과인 해시 테이블의 경우는 반드시 충돌이 발생하게 된다.
만약, 충돌이 발생하지 않다고 할 경우 해시 테이블의 탐색, 삽입, 삭제 연산은 모두 에 수행되지만 충돌이 발생할 경우 탐색과 삭제 연산이 최악에 만큼 걸리게 된다. 이는 같은 인덱스에 모든 키 값과 데이터가 저장된 경우로 충돌이 전부 발생했음을 말한다.
따라서, 충돌을 최대한으로 줄여서 연산속도를 빠르게 하는 것이 해시 테이블의 핵심인데 이에 중요하게 작용하는 것이 바로 해시함수를 구현하는 해시 알고리즘이다. 해시 알고리즘이 견고하지 못하게 되면 해시함수로 도출된 값들이 같은 경우가 빈번하게 발생하게 되므로 잦은 충돌로 이어지게 되는 것이다.
결론적으로 해시 테이블의 중점사항은 충돌을 완화하는 것이며 방법으로는 2가지가 있다.
- 해시 테이블의 구조 개선
- 해시 함수 개선
이제 차근차근 알아보도록 하자.
충돌해결 1 : 해시 테이블의 구조 개선
Separate Chaining (분리 연결법)

체이닝이란 충돌이 발생했을 때 이를 동일한 버킷(Bucket)에 저장하는데 이를 연결리스트 형태로 저장하는 방법을 말한다.
위 그림을 보면 John Smith 와 Sandra Dee 의 인덱스가 152 로 충돌하게 된 경우인데, 이 때 Sandra Dee 를 John Smith 뒤에 연결함으로써 충돌을 처리하는 것을 볼 수 있다.
이러한 Chaining 방식은 해시 테이블의 확장이 필요없고 간단하게 구현이 가능하며, 손쉽게 삭제할 수 있다는 장점이 있다. 하지만 데이터의 수가 많아지면 동일한 버킷에 chaining되는 데이터가 많아지며 그에 따라 캐시의 효율성이 감소한다는 단점이 있다.
※ 참고
실제로 Java8의 Hash테이블은 Self-Balancing Binary Search Tree 자료구조를 사용해 Chaining 방식을 구현하였다.
아래 코드는 java 8의 HashTable의 get() 메소드이다.
코드를 살펴보면 index를 계산하고 동일한 버킷에서 for문을 통해 key에 해당하는 value를 얻어오는 것을 볼 수 있다.

체이닝을 통해 해시테이블을 구현했을 때의 시간복잡도는 어떻게 될까?
삽입의 경우 연결리스트에 추가하기만 하면 되기 때문에 상수 시간인 이 걸리지만 탐색과 삭제의 경우는 최악일 때 키 값의 개수인 에 대해 가 걸리게 된다. 하지만 최악의 경우 보다는 시간복잡도를 적재율을 이용해서 평균으로 표현하는 것이 일반적이다.
적재율 를 이라고 하면 이 말의 뜻은 곧 해시 테이블 내에 공간 대비 키 값들이 얼마나 있느냐, 즉 충돌할 여지가 얼마나 있느냐의 뜻이다. 이를 시간복잡도에 적용하면 이라고 하는데 정확한 증명은 찾을 수 없었다. 어쨌든 말의 의미를 파악했으니 이렇게 알아두자.
Open Addressing (개방 주소법)
원래라면 해시함수로 얻은 해시값에 따라서 데이터와 키값을 저장하지만 동일한 주소에 다른 데이터가 있을 경우 다른 주소도 이용할 수 있게 하는 기법이다.
즉, 추가적인 메모리를 사용하는 Chaining 방식과 다르게 비어있는 해시 테이블의 공간을 활용하는 방법이다

위에서 살펴본 동일한 충돌에 대해서 이번엔 Chaining 방식을 적용하지 않고 그 다음으로 비어있는 주소인 153 에 저장하는 것을 볼 수 있다. 이러한 원리로 탐색, 삽입, 삭제가 이루어지는데 다음과 같이 동작한다.
- 삽입: 계산한 해시 값에 대한 인덱스가 이미 차있는 경우 다음 인덱스로 이동하면서 비어있는 곳에 저장한다. 이렇게 비어있는 자리를 탐색하는 것을 탐사(Probing)라고 한다.
- 탐색: 계산한 해시 값에 대한 인덱스부터 검사하며 탐사를 해나가는데 이 때 “삭제” 표시가 있는 부분은 지나간다.
- 삭제: 탐색을 통해 해당 값을 찾고 삭제한 뒤 “삭제” 표시를 한다.
- Open Addressing에서 데이터를 삭제하면 삭제된 공간은 Dummy Space로 활용되는데, 그렇기 때문에 Hash Table을 재정리 해주는 작업이 필요하다고 한다.
이러한 open addressing 방식은 3가지 방법을 통해서 해시 충돌을 처리한다.
Open Addressing의 3가지 충돌 처리기법
선형탐사(Linear Probing)

선형탐사는 가장 기본적인 충돌 해결기법으로 위에서 설명한 기본적인 동작방식이다. 선형탐사는 바로 인접한 인덱스에 데이터를 삽입해가기 때문에 데이터가 밀집되는 클러스터링(Clustering) 문제가 발생하고 이로 인해 탐색과 삭제가 느려지게 된다.
제곱탐사(Quadratic Probing)

해시의 저장순서 폭을 제곱으로 저장하는 방식이다. 예를 들어 처음 충돌이 발생한 경우에는 1^2만큼 이동하고 그 다음 계속 충돌이 발생하면 2^2, 3^2 칸씩 옮기는 방식이다.
선형탐사에 비해 더 폭넓게 탐사하기 때문에 탐색과 삭제에 효율적일 수 있다. 하지만 이는 초기 해시값이 같을 경우 탐사할 때 역시나 클러스터링(Clustering) 문제가 발생하게 된다.
이중해싱(Double Hashing Probing)
이중해싱은 선형탐사와 제곱탐사에서 발생하는 클러스터링 문제를 모두 피하기 위해 도입된 것이다.
처음 해시함수로는 해시값을 찾기 위해 사용하고 두번째 해시함수는 충돌이 발생했을 때 탐사폭을 계산하기 위해 사용되는 방식이다.
즉, 해시된 값을 한번 더 해싱하여 해시의 규칙성을 없애버리는 방식이다. 해시된 값을 한번 더 해싱하여 새로운 주소를 할당하기 때문에 다른 방법들보다 많은 연산을 하게 된다.
비교
| 장점 | 단점 | |
| Open Addressing | 해시충돌이 일어날 가능성이 적기 때문에 데이터의 개수가 작을수록 속도가 빨라진다. 연속된 공간에 데이터를 저장하기 때문에 캐시 효율이 좋아진다. |
해시충돌이 발생하면 해당 객체의 인덱스 값이 바뀌어 버린다. 부하율(load factor) 즉, 테이블에 저장된 데이터의 개수가 많아질수록(=밀도가 높아질수록) 성능이 급격히 저하된다. |
| Separate Chaining | 해시충돌이 일어나더라도 연결리스트로 노드가 연결되기에 index가 변하지 않는다. 테이블의 각 인덱스는 연결리스트로 구현되기 때문에 데이터 개수의 제약을 거의 받지 않는다. |
부하율(load factor)에 따라 선형적으로 성능이 저하 됨. 즉, 부하율이 작을 경우 에는 Open Addressing 방식이 빠르다. |
그럼 Java에서는 무엇을 채택했을까?.. 바로 Separate Chaining이다.
그리고 마지막으로 몇 가지만 더 설명하고 가도록 하겠다.
위에서 설명했듯이 부하율(load factor)에 대해 말하자면, 보통 데이터가 0.7~0.8(70% ~ 80%) 정도 채워질 경우 성능이 저하된다고 한다. 그래서 Java에서도 load factor 값을 0.75 로 두고 있다.
위키피디아에서 다음과 같이 그래프로 보여주고 있다. (참고 자료로만 보면 된다.)

위에서 배운 충돌 해결기법들을 비교해보면 적재율인 에 따라서 위와 같이 나오는데, 여기서 successful search는 찾고자 하는 데이터가 해시테이블에 있는 경우이고 unsuccessful search는 없는 경우이다.
또한 최악의 경우 해시충돌에 의해 한 개의 인덱스에 여러개의 노드가 연결 될 경우도 있다. 자바 내부에서는 이럴 경우 해당 인덱스의 LinkedList를 Binary Tree(이진트리)로 변환하여 데이터의 색인 속도를 높인다.
충돌해결 2 : 해시 함수 개선
위에서 해시 테이블에 사용되는 대표적인 해시 함수로는 4가지를 소개하였다.
| 해시 함수 | 설명 |
| Division Method | 나눗셈을 이용하는 방법으로 입력값을 테이블의 크기로 나누어 계산한다. ( 주소 = 입력값 % 테이블의 크기) 테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 알려져 있다. |
| Digit Folding | 각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다. |
| Multiplication Method | 숫자로 된 Key값 K와 0과 1사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같은 계산을 해준다. h(k)=(kAmod1) × m |
| Univeral Hashing | 다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법이다. |
이 4가지 방법 역시 해시 충돌을 해결하기 위해 개선하는 과정을 거쳐 탄생했다고 할 수 있겠다.
간단하게 Division Method, Multiplication Method 이 두 방법을 살펴보자.
나눗셈법(Division Method)
아주 간단하게 해시값을 구하는 방법으로 미리 해시 테이블의 크기인 을 아는 경우에 사용할 수 있다. 해시함수를 적용하고자 하는 값을 으로 나눈 나머지를 해시값으로 사용하는 방법이다. 즉 다음과 같다.

여기서 은 2의 제곱수을 사용하면 안된다고 하는데 이는 그 제곱수 2^p 로 나타날 때 의 하위 개의 비트를 고려하지 않는다고 한다. 따라서 은 소수(Prime Number)를 사용하는 것이 좋다.
곱셈법(Multiplication Method)
0 < A < 1 인 A 에 대해서 다음과 같이 구할 수 있다.

의 의미는 의 소수점 이하 부분을 말하며 이를 에 곱하므로 0부터 사이의 값이 된다. 이 방법의 장점은 이 어떤 값이더라도 잘 동작한다는 것이며 를 잘 잡는 것이 중요하다.
이외에도 다양한 해시 함수가 있다는 것만 알아두도록 하자.
구현
구조는 체이닝을 사용했고 해시 함수로는 아스키코드를 더하는 방식을 이용했다.
import java.util.LinkedList;
class Node{
private String key;
private String value;
public Node(String key, String value){
this.key = key;
this.value = value;
}
public String getKey() {
return key;
}
public void setKey(String key) {
this.key = key;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
}
class HashTable{
private LinkedList<Node>[] data;
public HashTable(int size){
data = new LinkedList[size];
}
// 입력 받은 key 값의 아스키 값을 더하여 해시값 생성
public int getHashCode(String key){
int hashCode = 0;
for(char c : key.toCharArray()){
hashCode += c;
}
return hashCode;
}
// 해시값을 배열의 인덱스로 변환
public int convertToIndex(int hashCode){
return hashCode % data.length;
}
// 배열 인덱스를 찾은 후 해당 배열에 여러 노드가 존재할 경우. 검색 key에 매핑되는 노드 검색
public Node searchKey(LinkedList<Node> list, String key){
if(list == null) return null;
for(Node node : list){
if(node.getKey().equals(key)){
return node;
}
}
return null;
}
public void put(String key, String value){
int hashCode = getHashCode(key);
int index = convertToIndex(hashCode);
System.out.println(key + ", hashCode(" + hashCode + "), index(" + index + ")");
LinkedList<Node> list = data[index];
if(list == null){
list = new LinkedList<Node>();
data[index] = list;
}
Node node = searchKey(list, key);
if(node == null){
list.addLast(new Node(key, value));
}else{
node.setValue(value);
}
}
public String get(String key){
int hashCode = getHashCode(key);
int index = convertToIndex(hashCode);
LinkedList<Node> list = data[index];
Node node = searchKey(list, key);
return node == null? "Not Found" : node.getValue();
}
}
public class Test {
public static void main(String[] args) {
HashTable h = new HashTable(3);
h.put("sung", "She is pretty");
h.put("jin", "She is a model");
h.put("hee", "She is an angel");
h.put("min", "She is cute");
System.out.println(h.get("sung"));
System.out.println(h.get("jin"));
System.out.println(h.get("hee"));
System.out.println(h.get("min"));
// 데이터가 없는 경우
System.out.println(h.get("jea")); // Not Found
// 기존 데이터 덮어씌기
h.put("sung", "She is beautiful");
System.out.println(h.get("sung"));
}
}sung, hashCode(445), index(1)
jin, hashCode(321), index(0)
hee, hashCode(306), index(0)
min, hashCode(324), index(0)
She is pretty
She is a model
She is an angel
She is cute
Not Found
sung, hashCode(445), index(1)
She is beautiful
해시테이블(HashTable) 시간복잡도
각각의 Key값은 해시함수에 의해 고유한 index를 가지게 되어 바로 접근할 수 있으므로 평균 O(1)의 시간복잡도로 데이터를 조회할 수 있다. 하지만 데이터의 충돌이 발생한 경우 Chaining에 연결된 리스트들까지 검색을 해야 하므로 O(N)까지 시간복잡도가 증가할 수 있다.
충돌을 방지하는 방법들은 데이터의 규칙성(클러스터링)을 방지하기 위한 방식이지만 공간을 많이 사용한다는 치명적인 단점이 있다.
만약 테이블이 꽉 차있는 경우라면 테이블을 확장해주어야 하는데, 이는 매우 심각한 성능의 저하를 불러오기 때문에 가급적이면 확정을 하지 않도록 테이블을 설계해주어야 한다.
※ 참고
통계적으로 해시 테이블의 공간 사용률이 70% ~ 80%정도가 되면 해시의 충돌이 빈번하게 발생하여 성능이 저하되기 시작한다고 한다.
또한 해시 테이블에서 자주 사용하게 되는 데이터를 Cache에 적용하면 효율을 높일 수 있다. 자주 hit하게 되는 데이터를 캐시에서 바로 찾음으로써 해시 테이블의 성능을 향상시킬 수 있다.
Java의 HashMap(해시맵) vs HashTable(해시테이블)
Java 개발자라면 (Key,Value)로 저장하는 익숙한 자료구조인 HashMap이 있다. 그렇다면 Java에서 HashTable과 HashMap의 차이점은 무엇일까?
결론부터 말하자면
- 해시테이블(HashTable) : 병렬 처리를 하면서 자원의 동기화를 고려해야 하는 상황
- 해시맵(HashMap) : 병렬 처리를 하지 않거나 자원의 동기화를 고려하지 않는 상황
즉, 가장 핵심적인 차이로는 동기화 지원 여부에 있다.
// 해시테이블의 put
public synchronized V put(K key, V value) {
// Make sure the value is not null
if (value == null) {
throw new NullPointerException();
}
// Makes sure the key is not already in the hashtable.
Entry<?,?> tab[] = table;
int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length;
@SuppressWarnings("unchecked")
Entry<K,V> entry = (Entry<K,V>)tab[index];
for(; entry != null ; entry = entry.next) {
if ((entry.hash == hash) && entry.key.equals(key)) {
V old = entry.value;
entry.value = value;
return old;
}
}
addEntry(hash, key, value, index);
return null;
}
// 해시맵의 put
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}위의 코드에서 첫번째 put은 해시테이블의 put이며, 두번째 put은 해시맵의 put이다. 첫번째 해시테이블의 put에는 synchronized 키워드가 붙어있는 것을 확인할 수 있는데, 이것은 병렬 프로그래밍을 할 때 동기화를 지원해준다는 것을 의미한다. 이것은 해당 함수를 처리하는 시간이 조금 지연됨을 의미힌다.
차이점
1. 동기화 Synchronization
HashMap의 경우 동기화를 지원하지 않는다.
반면 다중 스레드 환경에서 HashTable은 동기화를 지원하기 때문에 실행 환경에 따라 구분하여 사용하면 된다.
※ 참고
vector의 상위 호환 개념인 ArrayList의 사용을 권장하듯, 새로운 버전인 HashMap을 주로 사용하고 동기화가 필요하면 ConcurrentHashMap을 사용하는 것이 더 좋은 방법이라고 한다.
구형인 HashTable은 동기화 처리라는 비용때문에 HashMap에 비해 느리다.
2. Thread-safe 여부
Hashtable은 Thread-safe하고, HashMap은 Thread-safe하지 않다.
따라서 멀티스레드 환경이 아니라면 Hashtable은 HashMap 보다 성능이 떨어진다.
3. Null 값 허용 여부
Hashtable은 key에 null을 허용하지 않지만, HashMap은 key에 null을 허용한다.
4. Enumeration 여부
HashMap은 저장된 요소들의 순회를 위해 Fail-Fast Iterator를 반환한다.(ConcurrentHashMap의 경우에는 Fail-Safe Iterator)
Hashtable은 같은 경우 Enumeration을 반환한다.
※ 참고
Fail-Fast Iterator : 말 그대로 빠른 에러를 발생시켜 버그를 예방할 수 있다.
반면에 Enumeration를 사용한 코드는 중간에 remove를 해도 예외가 발생하지 않는다. 그렇기 때문에 나중에 버그를 발견하지 못할 확률도 존재한다.
5. 보조 해시 사용
HashMap은 보조해시를 사용하기 때문에 보조 해시 함수를 사용하지 않는 Hashtable에 비하여 해시 충돌(hash collision)이 덜 발생할 수 있어 상대적으로 성능상 이점이 있다.

요약
- 해시 맵은 기본 용량이 16개 요소인 버킷의 배열로, 각 버킷은 다른 해시 코드 값에 해당한다.
- 여러 개체가 동일한 해시 코드 값을 갖는 경우 단일 버킷에 저장된다.
- 로드 팩터에 도달하면 새 배열이 이전 배열의 두 배 크기로 생성되고 모든 요소가 새 해당 버킷으로 재할당된다.
- 값을 검색하려면 키를 해시 하고, 해당 버킷으로 찾아간다. 만약 해당 버킷에 둘 이상의 개체들이 있다면 LinkedList 탐색하듯이 탐색하게 된다.
참고