![[Linear Regression] Multi variable linear regression](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FoBrJ9%2Fbtq2kqDQsJz%2FgSqSg6U5z9YZXmmrAQKLpK%2Fimg.png)
모두의 딥러닝 시즌 2 정리...
현재까지 학습한 linear regression은 다음과 같다.
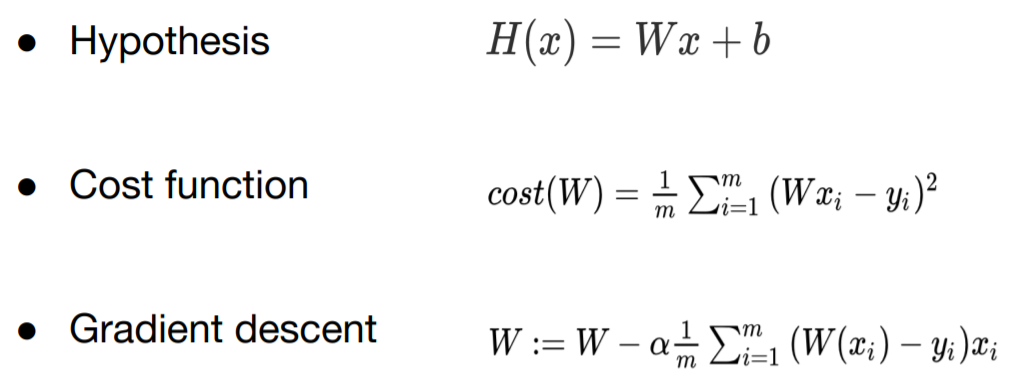
Hypothesis : 우리의 가설, 우리의 모델
Cost function : 우리의 예측과 실제의 차이를 제곱한 것의 평균. 제곱을 하는 이유는 마이너스를 배제하기 위해
Gradient descent : cost를 최소화하는 과정 => cost를 최소화하는 W, b를 찾는 과정. 즉, 학습 과정
Predicting exam score
예제로 시험의 점수를 예측하는 모델을 생각해보자.
아래의 그림은 입력이 1개이고 우리가 예측하려는 값도 1개이다. 이때 변수가 1개이고 이 변수를 Feature라고도 한다.
regression using one input (x)
One-variable(One-feature)
x가 공부한 시간 y가 시험 점수이며 하나의 변수에 대해서 하나의 예측치를 나타낸다.
여기서 생각해볼 것이 단순히 공부한 시간만을 갖고 예측하는 것보단 다양한 변수를 갖고 예측하는 것이 훨씬 더 예측을 잘할 수 있다고 생각해볼 수 있다.
아래는 시험 점수를 예측하는데 여러 개의 변수를 사용하는 모델을 위한 그림이다.
regression using three inputs (x1, x2, x3)
Multi-variable (Multi-feature)
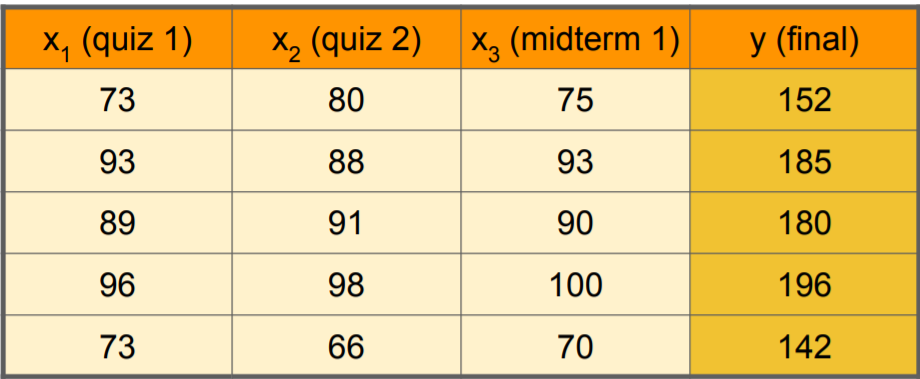
우리가 예측하고자 하는 것 기말 점수이고 우리는 기말고사를 보기 전에 여러 시험 봤을 것이다. (x1, x2, x3)
우리는 이것은 Multi-variable (Multi-feature)라고도 한다.
여기서 우리는 퀴즈 1, 퀴즈 2, 중간고사 점수를 통해 기말고사 점수를 예측해 볼 수 있고 새로운 학생의 퀴즈 1, 퀴즈 2, 중간고사 점수가 있다면 기말고사 점수를 예측해 볼 수 있을 것이다.
Hypothesis
우리는 변수가 하나일 때 우리의 가설 함수는 다음과 같이 정의하였다.
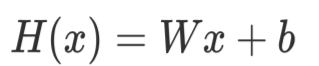
그렇다면 변수가 여러 개일 때 가설 함수는 어떻게 표현할 수 있을까?
변수가 여러 개이면 늘어난 변수만큼 기술하게 되며 변수가 늘어난 만큼 W(Weight, 가중치)를 필요로 하게 된다.
그래서 변수가 3개이면 W(Weight, 가중치)도 3개가 된다.
Cost Function
cost function은 이전과 크게 다르지 않고 동일하다.
Hypothesis를 동일하게 넣고 우리의 가설과 실제 값의 차이 제곱의 평균으로 동일한 수식을 갖는다.
Multi-variable(Multi-feature)
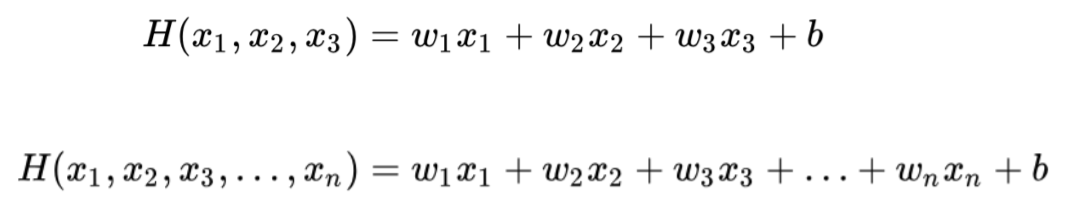
여기까지 확인해본바 결국 Multi-variable(Multi-feature)인 상황에서 우리의 가설은 늘어난 만큼 W(Weight, 가중치)도 늘어나는 것을 확인해 볼 수 있다.
Matrix multiplication
하지만 위에서 보이는 단점으로는 만약 변수의 개수가 수 백개, 수 천 개라면 위의 수식을 일일이 쓰는 것은 매우 불편할 것이다.
그래서 이때 등장하는 것이 Matrix이다.
우리는 이 문제를 해결하기 위해서 사용해 볼수 있는 것이 Matrix multiplication이다.
위의 그림처럼 두개의 Matrix가 있을 때 결과 값인 첫 번째 행, 첫 번째 칼럼의 값(즉, 58)은 첫 번째 Matrix의 행과 두 번째 Matrix의 열을 개별 값을 곱해서 모두 더해준 값이다. (1 × 7 + 2 × 9 + 3 × 11)
이 Matrix multiplication. 즉, Matrix의 곱셈 연산을 Dot Product라고 한다.
Hypothesis using matrix
이제 위에서 배운 Dot Product를 이용하면 Hypothesis를 길게 작성하지 않아도 간편하게 표현할 수 있다.
X : x로 구성된 Matrix
W : w(가중치)로 구성된 Matrix
(일반적으로 Matrix는 대문자로 표현)
이제 우리는 작성하기 귀찮은 수식이 아닌 이 두 개의 X, W Matrix를 통해 Hypothesis = XW와 같이 간편하게 표현할 수 있다.
※
눈치 빠른 사람은 알아챘겠지만 우리는 지금까지 w를 x 값 앞에 작성하였다.
그런데 위의 Matrix를 이용한 표현에서는 X가 W의 앞에 위치하게 된다.
그 이유는 Matrix 연산을 할 때 앞에 오는 Matrix의 행과 뒤에 오는 Matrix의 열을 함께 연산하기 때문에 X가 앞에 오고 W가 뒤에 오는 이런 형태가 되는 것이다.
이제는 예제를 이용해 우리의 Hypothesis함수를 Matrix를 이용해서 표현해 보겠다.
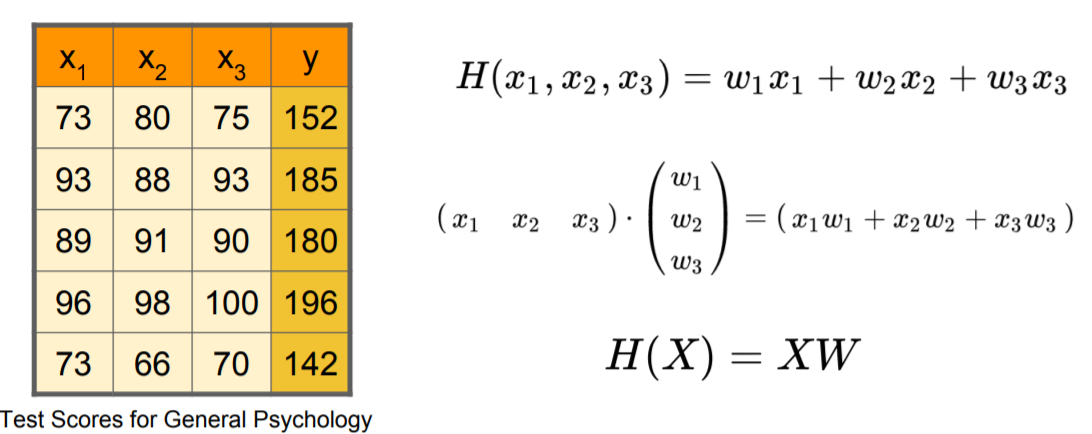
x1, x2, x3 점수가 주어졌을 때 해당 변수만큼의 w 값이 필요하며 우리는 Matrix를 통해 H(X) = XW와 같이 간편하게 표현이 가능해졌다.
Many x instances
Matrix를 이용한 표현에는 또 다른 장점이 있다. 아래의 예제는 총데이터의 개수가 5개임을 우리는 확인할 수 있다.
하지만 데이터의 갯수가 5...10...100 개인 것과 상관없이 우리는 동일하게 표현이 가능하다.
총 5건의 데이터가 준비되었을 때 w는 3개, 변수는 x1, x2, x3로 3개이다. 하지만 위에서 보이다시피 데이터가 얼마나 많든 간에 우리의 hypothesis는 matrix 연산을 통해 간편하게 표현이 가능하다.
즉, Matrix를 사용하게 되면 feature(변수)의 갯수가 몇 개든 instance(데이터)의 개수가 몇 개든 상관없이 모두 동일하게
위의 식처럼 표현이 가능하다!!
Matrix를 사용할 때 주의할 점
Matrix를 사용할 때 주의할 점으로는 첫 번째 Matrix의 칼럼과 두 번째 Matrix의 행(low)이 일치해야 한다는 것이다.
즉, 위의 예제에서는 [5, 3]의 3과 [3, 1]의 3이 동일해야 한다.
Matrix를 사용하는 또 다른 큰 장점
또 Matrix를 사용하는 또 다른 큰 장점은 데이터의 갯수와 무관하다는 것이다.
위의 예제에서는 5개짜리로 가정을 했지만 결국 이 데이터의 갯수. 즉, Instance의 개수는 몇 개가 오든 상관이 없다.
우리가 여기서 결정해야 할 것은 컬럼의 개수. 즉, 변수의 개수이다.
이제 간단한 예제를 통해 위의 장점을 이해해보자.
위에서 말했다시피 우리에게 필요한 [? ,?]의 개수는 데이터의 개수와 전혀 관련이 없이 입력 Matrix의 칼럼과 출력 Matrix의 칼럼만 알면 충분히 예측이 가능하다.
출력 개수가 몇개이건 입력 데이터의 개수가 몇 개이건 우리의 수식은 항상 XW로 변함이 없음을 기억하자.
WX vs XW
헷갈리만한 사항을 말해보고자 한다.
우리는 이론적으로는 W가 계수이기 때문에 WX와 같은 표현을 사용하였다. 하지만 TensorFlow 코드에서는 XW와 같이 사용한다.
그 이유는 XW가 Matrix multiplication으로 연산. 즉, X의 컬럼과 W의 행이 동일해야 하기 때문에 XW로 사용한다.
이제 해당 개념을 바탕으로 텐서플로우 라이브러리를 활용하여 구현해보도록 하겠다.