Stack
자료 구조 중 하나인 Stack의 사전적 정의는 '쌓다', '더미'라는 의미를 갖고 있다. 상자에 물건을 쌓아 올리듯이 데이터를 쌓는 자료 구조라고 할 수 있다.
Stack은 '마지막에 추가된 데이터가 가장 먼저 나오는' 특징을 가지고 있는 후입선출 LIFO(Last In First Out)의 자료구조다. 시간복잡도는 push O(1) , pop O(1) 이다. 활용 예시는 후위 표기법 연산, 괄호 유효성 검사, 웹 브라우저 방문기록(뒤로 가기), 깊이우선탐색(DFS) 등이 있다.
- 스택의 입출력은 맨 위에서만 일어나기 때문에 스택의 중간에서는 데이터를 삭제하는 것이 불가능 하다
- 스택이 입출력이 이루어지는 부분을 스택 상단(Stack top) , 바닥 부분을 스택 하단(Stack bottom) , 스택에 저장되는 것을 요소(Element) 라 부르며 스택에 요소가 하나도 없을 때 그러한 스택을 공백 스택(Empty stack) 이라고 한다.

push & pop
stack에서 데이터를 추가하는 것을 push라고 하고 데이터를 추출 하는 것은 pop이라고 한다. push의 경우 stack의 맨 뒤에 데이터를 추가하면 완료되기 때문에 시간복잡도는 O(1)이다. 이와 동일하게 pop의 경우도 맨 뒤의 데이터를 삭제하면 완료 되기 때문에 O(1)의 시간복잡도를 갖는다. push와 pop은 모두 stack의 top에 원소를 추가하거나 삭제하는 형식으로 구현된다.
Stack의 특징
- 먼저 들어간 자료가 나중에 나옴 LIFO(Last In First Out) 구조
- 시스템 해킹에서 버퍼오버플로우 취약점을 이용한 공격을 할 때 스택 메모리의 영역에서 함
- 인터럽트처리, 수식의 계산, 서브루틴의 복귀 번지 저장 등에 쓰임
- 그래프의 깊이 우선 탐색(DFS)에서 사용
- 재귀적(Recursion) 함수를 호출 할 때 사용
- 후위 표기법 연산, 괄호 유효성 검사, 웹 브라우저 방문기록(뒤로 가기)
Stack 사용법
Stack 선언
import java.util.Stack; //import
Stack<Integer> stack = new Stack<>(); //int형 스택 선언
Stack<String> stack = new Stack<>(); //char형 스택 선언자바에서 stack을 선언하려면 mport java.util.Stack 을 import 한 뒤 Stack<Element> stack = new Stack<>();과 같은 형식으로 선언하면 된다.
Stack 값 추가
Stack<Integer> stack = new Stack<>(); //int형 스택 선언
stack.push(1); // stack에 값 1 추가
stack.push(2); // stack에 값 2 추가
stack.push(3); // stack에 값 3 추가Stack에 값을 추가하고 싶다면 push(value)라는 메소드를 활용하면 된다. Stack에 위의 예제와 같이 값을 계속해서 추가해나간다면 아래 그림처럼 데이터가 쌓이게 된다.
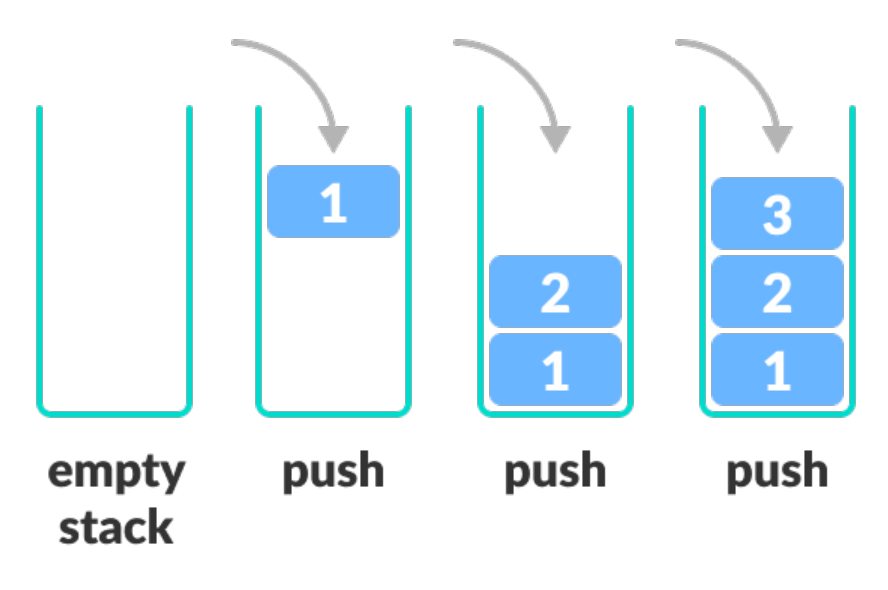
Stack 값 삭제
Stack<Integer> stack = new Stack<>(); //int형 스택 선언
stack.push(1); // stack에 값 1 추가
stack.push(2); // stack에 값 2 추가
stack.push(3); // stack에 값 3 추가
stack.pop(); // stack에 값 제거
stack.clear(); // stack의 전체 값 제거 (초기화)스택에서 값을 제거하고싶다면 pop()이라는 메서드를 사용하면 된다. pop을 하면 가장 위쪽에 있는 원소의 값이 아래 그림과 같이 제거된다. 스택의 값을 모두 제거하고싶다면 clear()라는 메서드를 사용하면 된다.
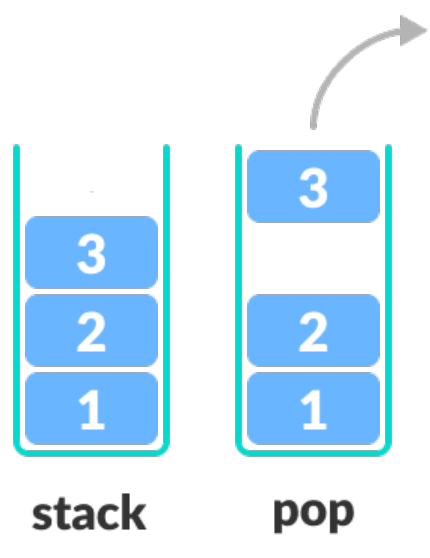
Stack의 가장 상단의 값 출력
Stack<Integer> stack = new Stack<>(); //int형 스택 선언
stack.push(1); // stack에 값 1 추가
stack.push(2); // stack에 값 2 추가
stack.push(3); // stack에 값 3 추가
stack.peek(); // stack의 가장 상단의 값 출력스택의 가장 위에 있는 값을 출력하고 싶다면 peek()라는 함수를 사용하면 된다. 아래 그림과 같이 가장 마지막에 들어간 값이 출력된다.

Stack의 기타 메서드
Stack<Integer> stack = new Stack<>(); //int형 스택 선언
stack.push(1); // stack에 값 1 추가
stack.push(2); // stack에 값 2 추가
stack.size(); // stack의 크기 출력 : 2
stack.empty(); // stack이 비어있는제 check (비어있다면 true)
stack.contains(1) // stack에 1이 있는지 check (있다면 true)그 밖에도 stack에는 크기를 구하는 size()메서드와 stack이 비어있는지 확인하는 empty() 메서드(비어있다면 true, 그렇지 않다면 false를 return) stack의 값을 search하는 contains(int value)함수가 있다.
Stack 클래스는 deprecated 되었다
우선 결론부터 말하자면 만일 어플리케이션에 스택 자료 구조를 사용해야 할 상황일때, 자바의 스택 클래스는 쓰기를 지양하여야 한다. 왜냐하면 Vector 컬렉션을 상속을 받아 구현되었기 때문인데, 이 Vector 클래스 자체가 컬렉션 프레임워크라는 개념이 나오기도 전에 자바 버전1 서부터 있었던 굉장히 오래된 클래스이기 때문에 여러모로 취약점이 많고, 또한 상속으로 인한 부모 메서드 공유 문제 때문에 사용자가 잘못되게 사용될 수 있다는 큰 문제점이 있기 때문이다.
즉, 자식 클래스에게는 부적합한 부모 클래스의 메소드가 상속되기 때문에 자식 클래스 인스턴스의 상태가 불안정해지게 된다는 문제점이 있다.
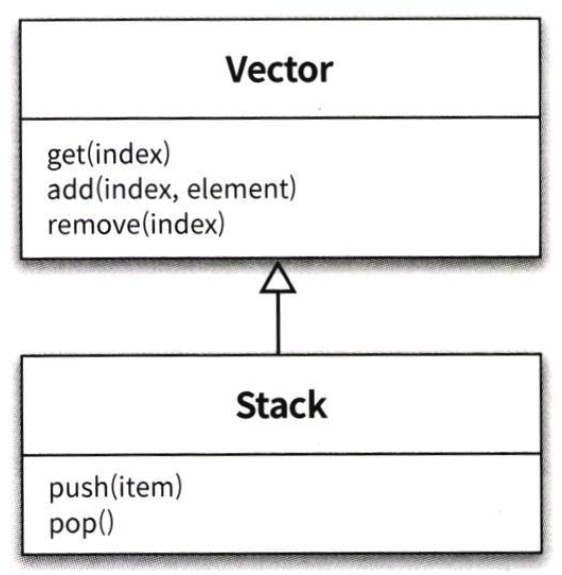
예를 들어 Stack의 대표적인 동작은 push, pop 이지만, 상속한 Vector 클래스의 add 메소드 또한 외부로 노출되게 된다. 그러면서 아래와 같이 개발자가 add 메소드도 스택 클래스에서 사용할수 있는 메소드인줄 알고 사용했다가, 의도치 않은 동작이 실행되면서 오류를 범하게 된다.
Stack<String> stack = new Stack<>();
stack.push("one");
stack.push("two");
stack.push("three");
stack.add(0, "four"); // add 메소드를 호출함으로써 stack의 의미와는 다르게 특정 인덱스의 값이 추가
// 마지막에 넣은 요소는 "four" 인데 스택은 "three"로 뽑혀진다
String str = stack.pop(); // three
System.out.println(str.equals("four")); // falseStack 대신 Deque 사용
따라서 자바 공식 문서에 보면 애초부터 상속을 잘못하여 잘못 설계된 Stack 클래스보다 Deque 클래스를 사용하여 구현할 것을 권장하고 있다.
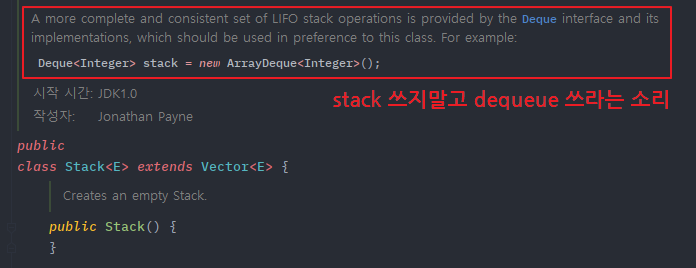
Deque(덱) 생소할지 모르겠지만, 양방향으로 넣고 꺼낼수 있는 향상된 큐(queue) 자료구조 쯤으로 이해하면 된다. 그래서 상황에 따라서 큐처럼 사용할 수도 있고 스택 처럼 유연하게 사용할수 있다.
/* Stack 처럼 사용하기 */
Deque<String> stack = new ArrayDeque<>();
stack.push("a");
stack.push("b");
stack.push("c");
stack.push("d");
stack.push("e");
System.out.println(stack); // [a, b, c, d, e]
System.out.println(stack.pop()); // e
System.out.println(stack.pop()); // d
System.out.println(stack); // [a, b, c]/* Queue 처럼 사용하기 */
Deque<String> queue = new ArrayDeque<>();
queue.offer("a");
queue.offer("b");
queue.offer("c");
queue.offer("d");
queue.offer("e");
System.out.println(queue); // [a, b, c, d, e]
System.out.println(queue.poll()); // a
System.out.println(queue.poll()); // b
System.out.println(queue); // [c, d, e]
번외) Stack 두 개를 이용하여 Queue를 구현해 보세요
queue의 enqueue()를 구현할 때 첫 번째 stack을 사용하고, dequeue()를 구현할 때 두 번째 stack을 사용하면 queue를 구현할 수 있다.
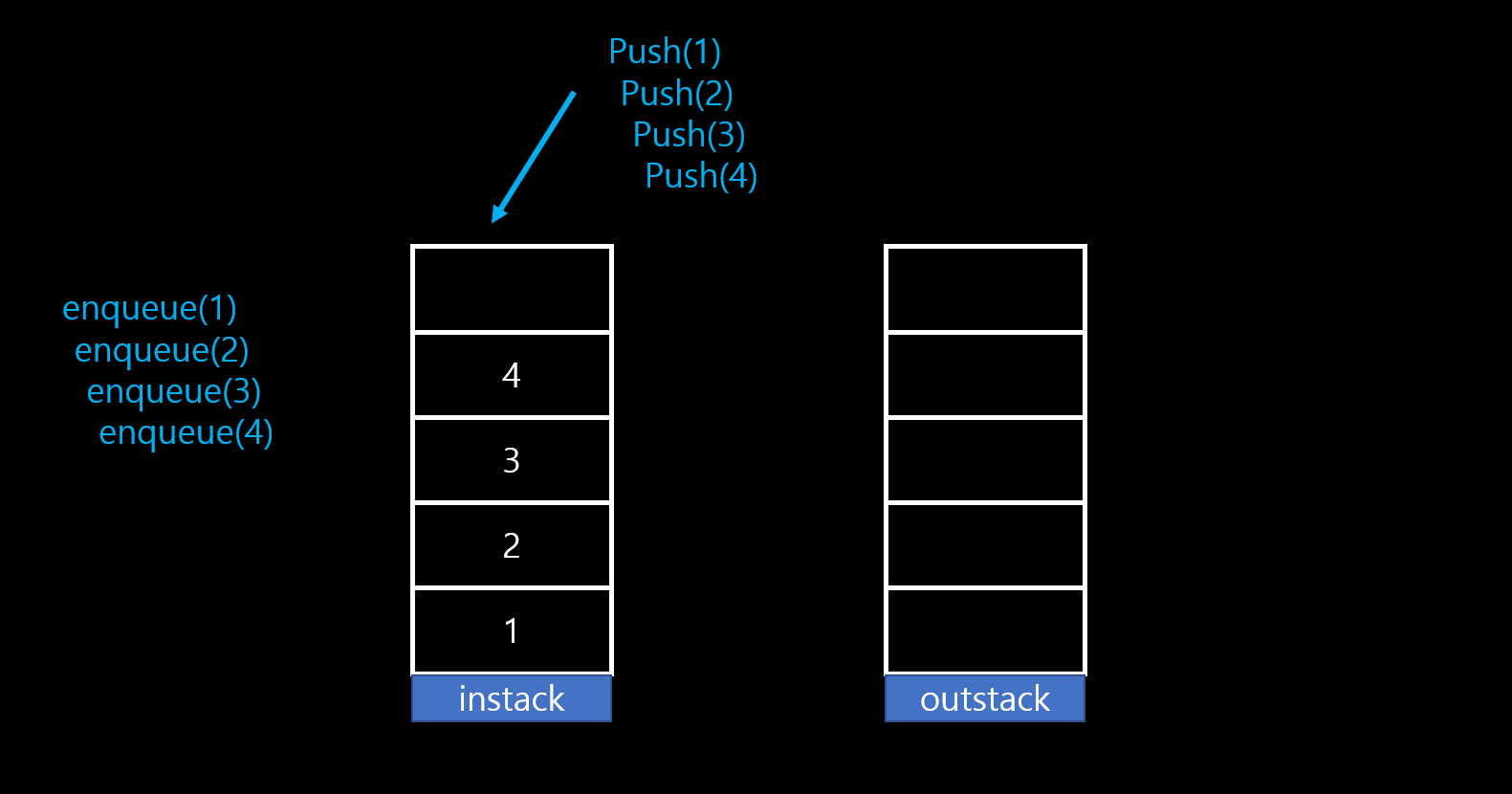
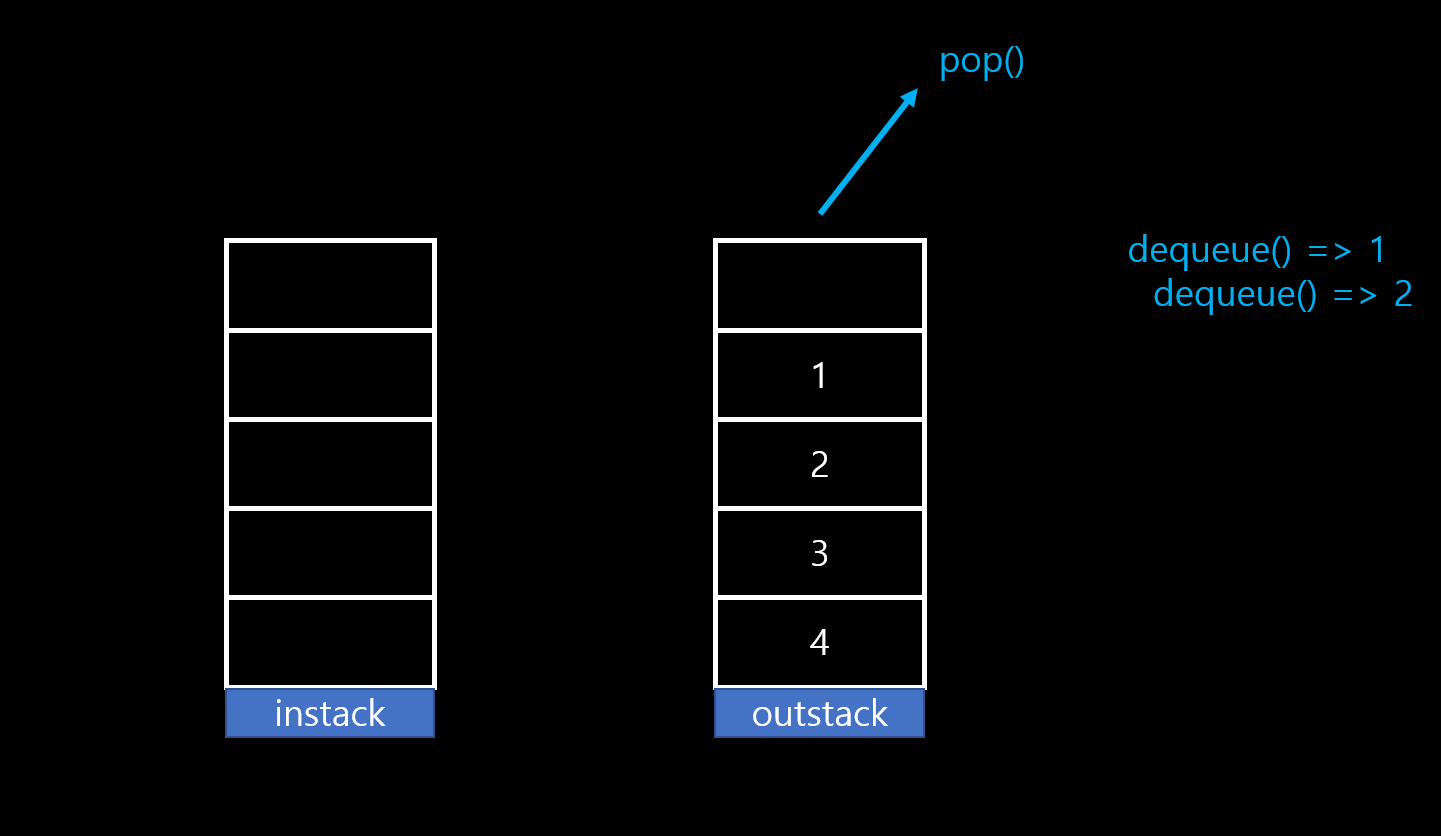
편의상 enqueue()에 사용할 stack을 instack이라고 부르고 dequeue()에 사용할 stack을 outstack이라고 칭하겠다. 두 개의 stack으로 queue를 구현하는 방법은 다음과 같다.
enqueue()
instack에 push()를 하여 데이터를 저장.
dequeue()
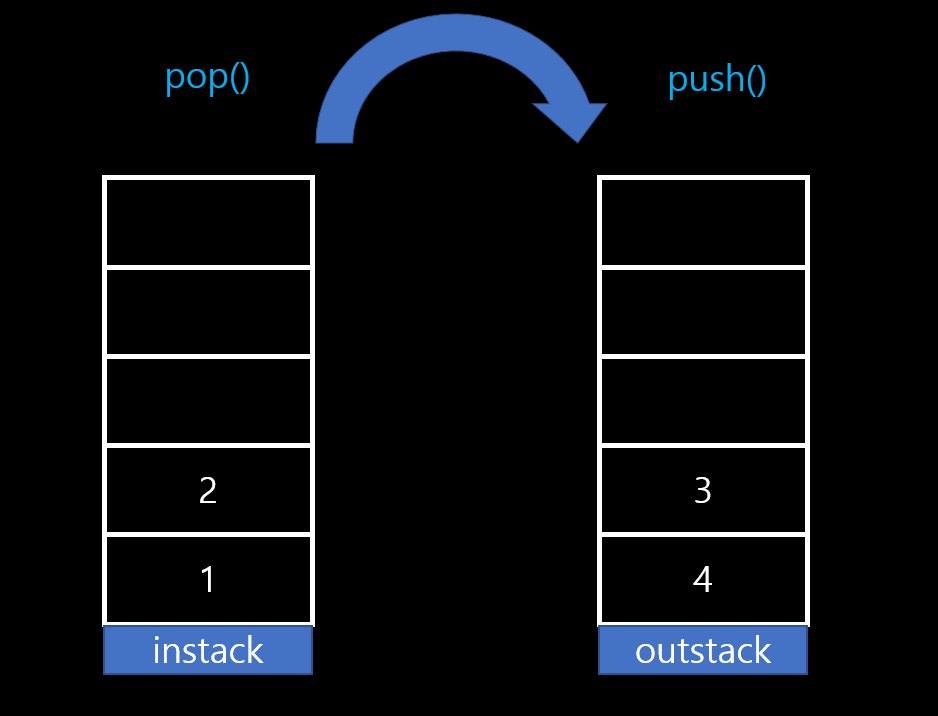
만약 outstack이 비어 있다면 instack.pop() 을 하고 outstack.push()를 하여 instack에서 outstack으로 모든 데이터를 옮겨 넣습니다. 이 결과로 가장 먼저 왔던 데이터는 outstack의 top에 위치하게 된다.
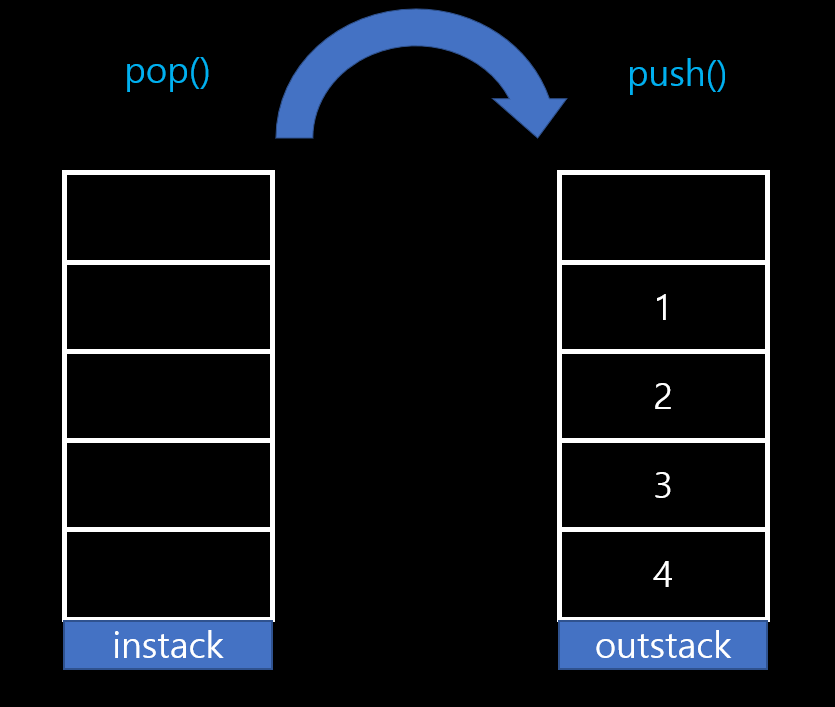
outstack.pop()을 하면 가장먼저 왔던 데이터가 가정 먼저 추출된다.(FIFO)
시간복잡도
- enqueue()
- instack.push()를 한번만 하면 되기 때문에 시간복잡도 O(1)이다.
- dequeue()
- 두 가지 경우를 따져봐야 한다. worst case는 outstack이 비어있는 경우다. 이 때는 instack에 있는 n개의 데이터를 instack.pop()을 한 이후에 outstack.push()를 해줘야 한다. 따라서 총 2*n 번의 operation이 실행되어야 하므로 O(n)의 시간복잡도를 갖는다.
- 하지만 outstack이 비어있지 않는 경우에는 outstack.pop()만 해주면 된다. 이는 O(1)의 시간복잡도를 갖는다. 이를 종합했을 때, amortized O(1)의 시간복잡도를 갖는다고 할 수 있다.
enqueue() - O(1)
dequeue() - O(1)
Pseudocode
1. Enqueue Operation
Push every input element to the Stack#1
2. Dequeue Operation
If(Stack#2 is empty)
pop every element in the Stack#1
and push them to the Stack#2 until Stack#1 is Empty
pop from Stack#2
3. 구현 예제
import java.util.Stack;
//2개의 Stack을 이용해서 Queue구현
class Qstack {
Stack<Integer> inStack;
Stack<Integer> outStack;
public Qstack() {
inStack= new Stack<>();
outStack= new Stack<>();
}
public void enqueue(int a) {
inStack.push(a);
}
public int dequeue() {
int result = -1;
if(outStack.isEmpty()) {
while(!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
result = outStack.pop();
}
//oldStack에 남아있는 값이 있으면 다시 #1로 옮겨준다.
if(!outStack.isEmpty()) {
while(!outStack.isEmpty()) {
inStack.push(outStack.pop());
}
}
return result;
}
}
public class Qs {
public static void main(String[] args) {
Qstack a = new Qstack();
a.enqueue(1);
a.enqueue(2);
a.enqueue(3);
System.out.println(a.dequeue());
System.out.println(a.dequeue());
System.out.println(a.dequeue());
}
}
참고